Структурные особенности учебного материала в школьном курсе геометрии

Рефераты / Математика / Структурные особенности учебного материала в школьном курсе геометрии

, , (3)

где – натуральные числа и . Заметьте, вовсе не утверждается обра

тное: что любые , получающиеся согласно (3) с натуральными , являются решением (1) и попарно взаимно просты. Решением эта тройка будет, но числа , , не обязательно получаются взаимно простыми. Ведь если у и есть общий делитель, то он войдет (даже с квадратом) и в , и в , и в .

Так что если бы настаивать на обратном утверждении, что любые , получающиеся согласно (3) с натуральными , будут решением (1) с попарно взаимно простыми , , , самое меньшее нужно бы уточнить: с взаимно простыми и . А было бы такого уточнения достаточно? Оказывается, нет. Ведь если и оба нечетные, то получится нечетным, а в (3) всегда четное. Но если одно из чисел четное, а другое нечетное, то получится нечетным, и общим с у него мог бы быть только нечетный делитель. Тогда у и имеется нечетный простой делитель . Раз делится на , то или делится на , а тогда, раз тоже делится на , то и второе из чисел делится на , т. е. и не взаимно просты, а мы уже решили, что будем брать только взаимно простые . Но главное, что этого сейчас не нужно. Надо только установить, что решение (1) с взаимно простыми натуральными , , обязательно представимо в виде (3) с какими-то а что при каких-то других могут получится решения с не взаимно простыми , , – это нас сейчас не касается.

Другое замечание состоит в том, что когда ограничиваться решениями с попарно взаимно простыми , , , то одно из чисел и должно быть четным, а другое – нечетным; при этом конечно, нечетно. Действительно, если и оба нечетные, то они не взаимно просты, а имеют общий делитель 2. Если же они оба нечетны, то можно написать, что , с некоторыми натуральными , . Отсюда

Получается, что делится на 2, но не делится на 4. Но это невозможно: если нечетно, то и на 2 не делится, а если четно, то делится на 4.

Раз одно из чисел и четно, а другое нечетно, то можно считать, что нечетно , а четно , – в противном случае просто изменим обозначения. Вот теперь начинается главное. Перепишем (1) так:

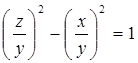
или, обозначая через и через , в виде , т. е. . и суть частные двух натуральных чисел, т. е. положительные рациональные числа (дроби). тоже рациональное число, причем положительное. Любое такое число представляется в виде несократимой дроби ; здесь и – натуральные числа, причем взаимно простые (раз дробь несократимая). А если