Структурные особенности учебного материала в школьном курсе геометрии

Т. д.

9. Второй признак равенства треугольников

Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

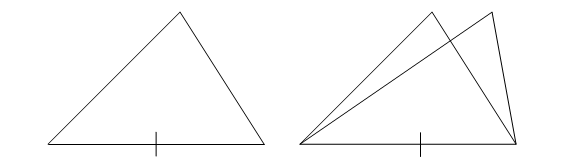
Дано: и , =, и =

Доказать: =

Доказательство

Пусть – треугольник, равный , с вершиной на луче , и вершиной в той же полуплоскости относительно прямой , где лежит вершина .

Так как , то вершина совпадает с вершиной. Так как , то луч совпадает с лучом , а луч совпадает с лучом . Отсюда следует, что вершина совпадает с вершиной . Итак совпадает с а значит, равен .

Т. д.

10. Третий признак равенства треугольников

Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

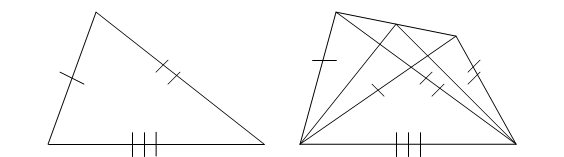
Дано: и , =, , .

Доказать: =

Доказательство

Допустим треугольники не равны, тогда у них , , . Иначе они были бы равны по первому признаку.

Пусть – треугольник, равный треугольнику , у которого вершина лежит в одной полуплоскости с вершиной , относительно прямой .

Пусть – середина отрезка . и – равнобедренные с общим основанием . Поэтому их медианы и являются высотами, значит прямые и перпендикулярны прямой .

Прямые и не совпадают, т. к. точки не лежат на одной прямой. Но через точку прямой можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию.

Т. д.

11. Первый признак параллелограмма

Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то такой четырехугольник – параллелограмм.

Дано: – четырехугольник, .

Доказать: – параллелограмм.

Доказательство

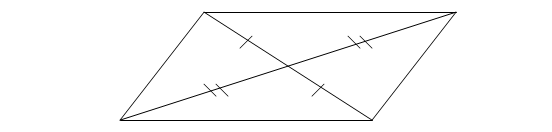
Рассмотрим и .

У них , как вертикальные, и – по условию, значит =, . А они являются внутренними накрест лежащими для прямых и и секущей .

По признаку параллельности прямых и параллельны.

Так же доказывается параллельность прямых и с помощью равенства треугольников и .

 Скачать реферат