Векторная алгебра и аналитическая геометрия
Определение. Вектором называется упорядоченная пара точек (начало вектора и его конец). Если ![]() ,
, ![]() , то вектор
, то вектор ![]() имеет координаты
имеет координаты ![]() .
.
Век
тор ![]() в координатном пространстве Oxyz, может быть представлен в виде
в координатном пространстве Oxyz, может быть представлен в виде
![]() , где тройка
, где тройка ![]() называется координатами вектора. Векторы
называется координатами вектора. Векторы ![]() – единичные векторы (орты), направленные в положительную сторону координатных осей Ox, Oy и Oz, соответственно. Длиной (модулем) вектора
– единичные векторы (орты), направленные в положительную сторону координатных осей Ox, Oy и Oz, соответственно. Длиной (модулем) вектора ![]() называется число
называется число ![]() .
.
Линейные операции с векторами
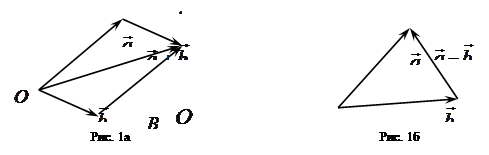 |
Сложение векторов определяется по правилу параллелограмма: вектор ![]() является диагональю параллелограмма, построенного на векторах
является диагональю параллелограмма, построенного на векторах ![]() и
и ![]() (рис.1а).
(рис.1а).
Разность двух векторов ![]() и
и ![]() определяется по формуле
определяется по формуле ![]() , где
, где ![]() – вектор той же длины, что и вектор
– вектор той же длины, что и вектор ![]() , но противоположно направленный. Чтобы найти вектор-разность
, но противоположно направленный. Чтобы найти вектор-разность ![]() нужно отложить векторы
нужно отложить векторы ![]() и
и ![]() из общей точки, соединить концы векторов вектором, направленным от «вычитаемого» к «уменьшаемому» (то есть от
из общей точки, соединить концы векторов вектором, направленным от «вычитаемого» к «уменьшаемому» (то есть от ![]() к
к ![]() ) (рис.1б). Построенный вектор и будет искомой разностью.
) (рис.1б). Построенный вектор и будет искомой разностью.
При сложении нескольких векторов каждая координата суммы есть сумма соответствующих координат слагаемых векторов, при умножении вектора на данное число ![]() на это же число умножаются и координаты вектора:
на это же число умножаются и координаты вектора:
а) ![]() ;
;
б) ![]() , где
, где ![]() – скалярный множитель.
– скалярный множитель.
Несколько векторов называются коллинеарными (компланарными), если они параллельны одной и той же прямой (плоскости). Векторы ![]() и
и ![]() параллельны (коллинеарны), то есть соответствующие координаты этих векторов пропорциональны с одним и тем же коэффициентом пропорциональности:
параллельны (коллинеарны), то есть соответствующие координаты этих векторов пропорциональны с одним и тем же коэффициентом пропорциональности: 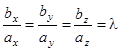 .
.
Базис на плоскости и в пространстве
Определение. Базисом на плоскости (в пространстве) называется упорядоченная пара (тройка) неколлинеарных (некомпланарных) векторов. Любой вектор однозначным образом раскладывается по базису. Коэффициенты разложения называются координатами этого вектора относительно данного базиса. Векторы ![]() образуют базис в декартовом координатном пространстве Oxyz.
образуют базис в декартовом координатном пространстве Oxyz.
Пример 1.
Даны векторы ![]() . Показать, что векторы
. Показать, что векторы ![]() и
и ![]() образуют базис на плоскости и найти координаты вектора
образуют базис на плоскости и найти координаты вектора ![]() в этом базисе.
в этом базисе.
Решение. Если два вектора неколлинеарны (![]() ), то они образуют базис на плоскости. Так как
), то они образуют базис на плоскости. Так как 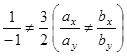 , то векторы
, то векторы ![]() и
и ![]() неколлинеарны и, значит, образуют базис. Пусть в этом базисе вектор
неколлинеарны и, значит, образуют базис. Пусть в этом базисе вектор ![]() имеет координаты
имеет координаты ![]() , тогда разложение вектора
, тогда разложение вектора ![]() по векторам
по векторам ![]() и
и ![]() имеет вид
имеет вид ![]() , или в координатной форме
, или в координатной форме
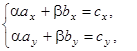 или
или ![]()
Решив полученную систему уравнений каким-либо образом, получим, что![]() .
.
Значит ![]() . Таким образом, в базисе
. Таким образом, в базисе ![]() вектор
вектор ![]() имеет координаты
имеет координаты ![]() .
.
Скалярное, векторное, смешанное произведение векторов.
Определение. Скалярным произведением двух векторов ![]() и
и ![]() называется число, определяемое равенством:
называется число, определяемое равенством:
![]() ,
,
где ![]() – угол между векторами
– угол между векторами ![]() и
и ![]() . Если
. Если ![]() , то
, то ![]() .
.
Зная скалярное произведение, можно определить угол между двумя векторами по формуле: 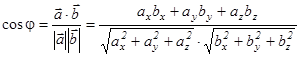 .
.
Условие перпендикулярности ненулевых векторов (угол между ними равен 90°) имеет вид: ![]() , или
, или ![]() , а условие их коллинеарности:
, а условие их коллинеарности: ![]() , или
, или 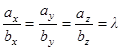 .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
