Нестандартные методы решения задач по математике

Так как , то

.

Однако известно, что . Отсюда следует, что , т.е. правая часть уравнения не превос

ходит . Ранее было доказано, что левая часть уравнения неотрицательна, поэтому равенство в может быть только в том случае, когда обе его части равны , а это возможно лишь при .

Ответ: .

9. Методы решения симметрических систем уравнений

В ряде случаев приходится решать системы уравнений с симметрическим вхождением слагаемых или сомножителей. Системы с таким свойством будем называть симметрическими. К таким системам относятся системы вида

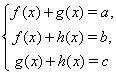
и

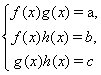
Метод решения системы состоит в сложении левых и правых частей уравнений. Тогда

заем из полученного уравнения поочередно вычитаются третье, второе и первое уравнения системы , в результате чего получается система уравнений

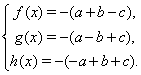
При решении системы уравнений необходимо перемножить левые и правые части уравнений, тогда получаем

Здесь необходимо потребовать, чтобы выполнялось условие . Если затем полученное уравнение разделить поочередно на третье, второе и первое уравнения системы , то получаем две системы уравнений относительно , , вида

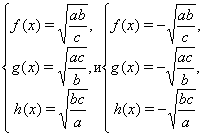
Полученные системы уравнений относительно , , допускают более простое решение по сравнению с решением систем уравнений , . Следует отметить, что данный метод обобщается на случай произвольного числа уравнений, содержащихся симметрических системах.

Кроме изложенного выше метода, существует еще много других, которые учитывают специфику заданной симметрической системы уравнений.

Задачи и решения

Пример 52 Решить систему уравнений

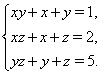
Решение. Если к обеим частям каждого уравнения системы прибавить 1, то получаем

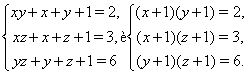
Из последней системы уравнений следует

Пусть , тогда

и , , .

Если , то по аналогии с предыдущим получаем , , .

Ответ: , , ; , , .

Пример 53 Решить систему уравнений

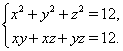
Решение. Из первого уравнения системы вычем второе уравнение, тогда . Умножим на обе части последнего уравнения и получим

откуда следует . В таком случае первое уравнение системы принимает вид . Следовательно, .Так как , то

Ответ: , , ; , , .

Пример 54 Решить систему уравнений

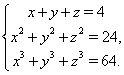
Решение. Обозначим и . Тогда из первого уравнения системы следует, что .

Преобразуем второе и третье уравнения системы следующим образом:

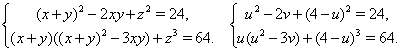
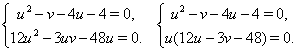
Из второго уравнения системы следует, что необходимо рассмотреть два случая.

1) Пусть . Тогда , а из первого уравнения системы получаем . Так как и , то имеет место система уравнений

 Скачать реферат