Нестандартные методы решения задач по математике

Ответ: .

Пример 4 Решить уравнение

Решение. Для преобразования левой части уравнения воспользуемся очевидным равенством . Тогда из уравнения имеем

<

img border=0 width=105 height=32 src="images/referats/655/image048.gif">

и

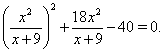
Если затем положить , то получим уравнение , корни которого равны и .

Таким образом, необходимо рассмотреть два уравнения и , т.е. и , где . Первое уравнение корней не имеет, а из второго получаем .

Ответ: , .

Пример 5 Решить уравнение

Решение. Первоначально убедимся, что не является корнем уравнения . Так как , то разделим обе части уравнения на . Тогда получим

Пусть , тогда

и из уравнения следует или . Последнее уравнение представим в виде . Отсюда следует, что и .

Далее, рассмотрим три уравнения , и . Первые два уравнения корней не имеют, а корнями третьего уравнения являются

Ответ:

Пример 6 Решить неравенство

Решение. Разделим числитель и знаменатель дроби в левой части неравенства на и обозначим через . Тогда неравенство можно переписать как

и

Решая неравенство с учетом того, что , получаем . Поскольку , то .

Ответ: .

Пример 7 Решить уравнение

Решение. Выполним замену переменных, пусть и . Так как и , тo . Кроме того, имеем .

В таком случае из уравнения получаем систему уравнений

Пусть теперь и , тогда из системы уравнений следует и . Отсюда с учетом того, что , получаем и . Следовательно, имеет место , и .

Поскольку и , то и , где --- целое число.

Ответ: , где --- целое число.

2. Метод тригонометрической подстановки

К числу, нестандартных методов решения алгебраических уравнений относится метод, основанный на применении тригонометрической подстановки. Использование такого метода целесообразно в том случае, когда искомые уравнения напоминают известные тригонометрические формулы. Это относится преимущественно к уравнениям (системам уравнений), решение которых обычными приемами весьма затруднительно, и которые после введения тригонометрических подстановок сводятся к несложным тригонометрическим уравнениям. Суть тригонометрической подстановки состоит в замене неизвестной переменной тригонометрической функцией, например или , а также в замене некоторой функцией от , или .

 Скачать реферат