Нестандартные методы решения задач по математике
Содержание
Введение
1. Метод функциональной подстановки
2. Метод тригонометрической подстановки
3. Методы, основанные на применении численных неравенств
4. Методы, основанные на монотонности функций
5. Методы решения функциональных уравнений
6. Методы, основанные на применении векторов
7. Комбинированные методы
8. Методы, основанные на
использовании ограниченности функций
9. Методы решения симметрических систем уравнений
10. Методы решения уравнений, содержащих целые или дробные части числа
Заключение
Литература
Введение
В настоящее время на занятиях по математике в математических классах общеобразовательных школ, гимназий и лицеев все большее внимание уделяется изучению нестандартных методов решения уравнений и неравенств из различных разделов математики (алгебра, тригонометрия и геометрия). В известной степени это вызвано тем, что в последние годы имеет место устойчивая тенденция к усложнению заданий, предлагаемых на вступительных экзаменах по математике в ведущих высших учебных заведениях Беларуси и Российской Федерации.
В данной работе предлагаются нестандартные методы решения задач по математике, которые имеют довольно-таки широкое распространение. Многие из приведенных здесь задач предлагались совсем недавно на вступительных экзаменах по письменной математике в Белгосуниверситете.
1. Метод функциональной подстановки
Метод функциональной подстановки является, пожалуй, самым распространенным методом решения сложных задач школьной математики. Суть метода состоит в введении новой переменной ![]() , применение которой приводит к более простому выражению. Частным случаем функциональной подстановки является тригонометрическая подстановка.
, применение которой приводит к более простому выражению. Частным случаем функциональной подстановки является тригонометрическая подстановка.
Основная трудность решения задач методом функциональной подстановки заключается в том, что зачастую трудно угадать вид самой подстановки и вид уравнений (или неравенств), где эту подстановку можно использовать. В настоящем разделе предлагаются наиболее распространенные уравнения и неравенства, которые эффективно решаются методом функциональной подстановки.
Задачи и решения
Пример 1 Решить уравнение
![]()
Решение. Введем новую переменную ![]() , тогда из получаем уравнение
, тогда из получаем уравнение ![]() . Поскольку обе части полученного уравнения неотрицательны, то после возведения в квадрат получаем равносильное уравнение
. Поскольку обе части полученного уравнения неотрицательны, то после возведения в квадрат получаем равносильное уравнение ![]() . Отсюда вытекает
. Отсюда вытекает ![]() ,
, ![]() и
и ![]() ,
, ![]() .
.
Рассмотрим два уравнения
![]()
Первое уравнение корней не имеет, а из второго получаем ![]() и
и ![]() . Подстановкой в убеждаемся в том, что найденные значения переменной
. Подстановкой в убеждаемся в том, что найденные значения переменной ![]() являются корнями исходного уравнения.
являются корнями исходного уравнения.
Ответ: ![]() .
.
Пример 2 Решить уравнение
![]()
Решение. Нетрудно видеть, что ![]() и
и ![]() является корнем уравнения.
является корнем уравнения.
Пусть теперь ![]() , тогда обе части уравнения разделим на
, тогда обе части уравнения разделим на ![]() и получим уравнение
и получим уравнение
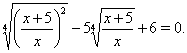
Если обозначить ![]() , то уравнение принимает вид квадратного уравнения
, то уравнение принимает вид квадратного уравнения ![]() , корнями которого являются
, корнями которого являются ![]() и
и ![]() .
.
Рассмотрим уравнения ![]() и
и ![]() , откуда следует, что
, откуда следует, что ![]() и
и ![]() . Так как
. Так как ![]() , то наиденные значения
, то наиденные значения ![]() являются корнями уравнения.
являются корнями уравнения.
Ответ: ![]() ,
, ![]() ,
, ![]() .
.
Пример 3 Решить уравнение
![]()
Решение. Перепишем уравнение в виде
![]()
Положим, что ![]() и
и ![]() , тогда из получим уравнение
, тогда из получим уравнение ![]() , из которого следует
, из которого следует ![]() и
и ![]() ,
, ![]() . Так как
. Так как ![]() и
и ![]() , то
, то ![]() и при этом
и при этом ![]() .
.
Поскольку ![]() и
и ![]() , то
, то ![]() . Отсюда получаем систему уравнений
. Отсюда получаем систему уравнений
![]()
где ![]() . Решением системы уравнений относительно
. Решением системы уравнений относительно ![]() является
является ![]() . Так как при этом
. Так как при этом ![]() и
и ![]() , то
, то ![]() и
и ![]() .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
