Нестандартные методы решения задач по математике

из которой следует , , и , border=0 width=45 height=23 src="images/referats/655/image053.gif">, .

2) Пусть , тогда . Если данрое выражение для подставить в первое уравнение ситемы , то получим квадратное уравнение относительно переменной вида , которое имеет два корня и .

Если , то и из первого уравнения системы получаем . В таком случае

и , , , , , .

Если , то , и

Отсюда следует , , , , , .

Ответ: См. выше.

Пример 55 При каких значениях параметра система неравенств

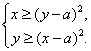
имеет единственное решение?

Решение. В систему неравенств переменные , входят симметрично, поэтому единственное ее решение необходимо искать в виде и , где .

Подставим в любое из неравенств системы , тогда или . Для того, чтобы квадратное неравенство имело бы единственное решение, необходимо его дискриминант приравнять нулю, т.е. , и .

Ответ: .

10. Методы решения уравнений, содержащих целые или дробные части числа

К числу нестандартных относятся методы решения уравнений, которые содержат целые и (или) дробные части действительных чисел. В программе школьной математики методы решения таких уравнений не изучаются. В настоящем разделе применение существующих методов и приемов иллюстрируется на примерах решения ряда уравнений.

Целой частью действительного числа (или Антье) называется наибольшее целое число, не превосходящее , и это число обозначается через . Очевидно, что . Разность называется дробной частью числа (или Мантисса) и обозначается через . Из определения следует, что . Кроме того, справедливо равенство

Например, имеет место , , , и , , .

Отметим некоторые свойства введенного выше понятия целой части действительного числа.

Для произвольных действительных чисел имеет место неравенство

Кроме того, для любого действительного числа справедливо

Перейдем теперь к рассмотрению уравнений, содержащих целую и (или) дробную части неизвестной перенной.

Задачи и решения

Пример 56 Решить уравнение

 Скачать реферат