Нестандартные методы решения задач по математике

Пример 60 Решить уравнение

Решение. Решая тригонометрическое уравнение , получаем

где --- целое число. Из уравнения получаем совокупность двух урав

нений или . Левые части обоих уравнений являются целыми числами, в то время как их правые части (за исключением случая в первом уравнении) принимают иррациональные значения.

Следовательно, равенство в уравнениях совокупности может иметь место только в том случае, когда правые их части являются рациональными (точнее, целыми) числами. А это возможно лишь в первом уравнении при условии, что . В этом случае получаем уравнение , откуда следует или .

Ответ: .

Пример 61 Решить уравнение

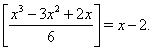
Решение. Левая часть уравнения принимает только целые значения, поэтому число является целым.

Так как , то при любом целом многочлен представляет собой произведение трех последовательно расположенных на числовой оси целых чисел, среди которых имеется хотя бы одно четное число и число, кратное трем. Следовательно, многочлен делится на без остатка, т.е. является целым числом.

В этой связи 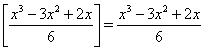и уравнение принимает вид или

Так как , то корнями уравнения являются , и .

Ответ: , , .

Пример 62 Доказать равенство

для произвольного действительного числа .

Доказательство. Любое число можно представить или как , или как , где --- целое число и .

Рассмотрим два возможных случая.

1) Пусть . Так как , то

и

.

2) Пусть , тогда

и

.

Таким образом, равенство выполняется для каждого из двух рассмотренных выше случаев. Следовательно, равенство доказано.

Заключение

Применение нестандартных методов решения задач по математике требует от старшеклассников и абитуриентов нетрадиционного мышления, необычных рассуждений. Незнание и непонимание таких методов существенно уменьшает область успешно решаемых задач по математике. Тем более, что имеющая место тенденция к усложнению конкурсных заданий по математике стимулирует появление новых оригинальных (нестандартных) подходов к решению математических задач. Следует отметить, что знание нестандартных методов и приемов решения задач по математике способствует развитию у старшеклассников нового, нешаблонного мышления, которое можно успешно применять также и в других сферах человеческой деятельности (кибернетика, вычислительная техника, экономика, радиофизика, химия и т.д.).

Литература

1. А.И.Назаров «Задачи-ловушки», Мн., «Аверсэв»,2006

2.С.А. Барвенов «Математика для старшеклассников», «Аверсэв»,2004

3. О.Н. Пирютко «Типичные ошибки на централизованном тестировании», Мн., «Аверсэв»,2006

4. С.А. Барвенов «Методы решения алгеброическиж уравнений», «Аверсэв»,2006

 Скачать реферат