Нестандартные методы решения задач по математике
Ответ: ![]() .
.
Пример 21 Решить уравнение
![]()
Решение. Введем новую переменную Уравнение имеет очевидный корень Так как Таким образом, имеем Ответ: Пример 22 Решить уравнение
Решение. Разделим обе части уравнения на Подбором нетрудно установить, что Обозначим Если Если Следовательно, среди Ответ: 5. Методы решения функциональных уравнений
К числу наиболее сложных задач на вступительных конкурсных экзаменах по математике относятся задачи, решение которых сводится к рассмотрению функциональных уравнений вида
или
где Методы решения функциональных уравнений , основаны на использовании следующих теорем.
Теорема 23 Корни уравнения Доказательство. Пусть Отсюда следует, что
т.е. Теорема 24 Если Доказательство. Пусть Так как Отсюда и из теоремы следует справедливость теоремы .
Следствие 25 Если функция ![]() . Тогда
. Тогда ![]() ,
, ![]()
![]() . Покажем, что других корней нет. Для этого разделим обе части уравнения на
. Покажем, что других корней нет. Для этого разделим обе части уравнения на ![]() , тогда
, тогда
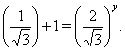
![]() , а
, а ![]() , то левая часть уравнения является убывающей функцией, а правая часть --- возрастающей функцией. Поэтому уравнение если имеет корень, так только один. Ранее было установлено, что
, то левая часть уравнения является убывающей функцией, а правая часть --- возрастающей функцией. Поэтому уравнение если имеет корень, так только один. Ранее было установлено, что ![]() --- корень уравнения . Следовательно, этот корень единственный.
--- корень уравнения . Следовательно, этот корень единственный.
![]() . Тогда единственным корнем уравнения является
. Тогда единственным корнем уравнения является ![]() .
.
![]() .
.
![]()
![]() , тогда
, тогда
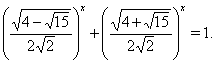
![]() является корнем уравнения . Покажем, что других корней это уравнение не имеет.
является корнем уравнения . Покажем, что других корней это уравнение не имеет.
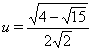 и
и 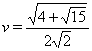 . Очевидно, что
. Очевидно, что ![]() . Следовательно, каждая из функций
. Следовательно, каждая из функций ![]() и
и ![]() является убывающей и при этом
является убывающей и при этом ![]() .
.
![]() , то
, то ![]() ,
, ![]() и
и ![]() .
.
![]() , то
, то ![]() ,
, ![]() и
и ![]() .
.
![]() 2 или
2 или ![]() корней уравнения нет.
корней уравнения нет.
![]() .
.
![]()
![]()
![]() ,
, ![]() ,
, ![]() --- некоторые функции и
--- некоторые функции и ![]() .
.
![]() являются корнями уравнения
являются корнями уравнения
![]() --- корень уравнения
--- корень уравнения ![]() , т.е.
, т.е. ![]() . Тогда справедливы равенства
. Тогда справедливы равенства
![]()
![]()
![]() является корнем уравнения .
является корнем уравнения .
![]() --- возрастающая функция на отрезке
--- возрастающая функция на отрезке ![]() и
и ![]() , то на данном отрезке уравнения и
, то на данном отрезке уравнения и ![]() равносильны.
равносильны.
![]() является корнем уравнения , т.е.
является корнем уравнения , т.е. ![]() . Предположим, что
. Предположим, что ![]() не является корнем уравнения
не является корнем уравнения ![]() , т.е.
, т.е. ![]() . He нарушая общности рассуждений, будем считать, что
. He нарушая общности рассуждений, будем считать, что ![]() . Тогда в силу возрастания функции
. Тогда в силу возрастания функции ![]() справедливы неравенства
справедливы неравенства
![]()
![]() , то из приведенных выше неравенств следует
, то из приведенных выше неравенств следует ![]() . Таким образом, получили ложное неравенство. А это означает, что
. Таким образом, получили ложное неравенство. А это означает, что ![]() .
.
![]() возрастает для любого
возрастает для любого ![]() , то уравнения и
, то уравнения и ![]() равносильны.
равносильны.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
