Типовой расчет
1. Найти сумму ряда:
![]()
Решение.
Разложим знаменатель на множители.
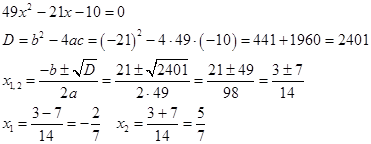
Значит,
![]()
Разложим дробь ![]() , используя
, используя
метод неопределённых коэффициентов.
![]()
то есть:
![]()
![]()
![]() ,
, ![]() ,
, ![]()
Следовательно,
![]()
Тогда, исходный ряд примет вид:
![]()
Найдём n – первые членов ряда, записывая дроби с одинаковыми знаменателями друг под другом:
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
Сложим n – первых членов ряда и найдём их сумму.
![]() .
.
Тогда искомая сумма равна:
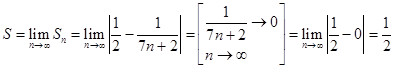 .
.
Ответ: ![]() .
.
2. Найти сумму ряда:
![]()
Решение.
Разложим дробь ![]() , используя метод неопределённых коэффициентов.
, используя метод неопределённых коэффициентов.
![]()
то есть:
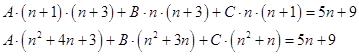
![]()
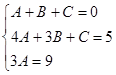 ,
, 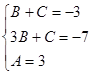 ,
, 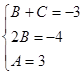 ,
, 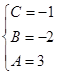
Следовательно,
![]()
Тогда, исходный ряд примет вид:
![]()
Найдём n – первых членов ряда ![]() , записывая дроби с одинаковыми знаменателями, друг под другом:
, записывая дроби с одинаковыми знаменателями, друг под другом:
![]() =
= ![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
Сложим n – первых членов ряда
![]()
и найдём их сумму.
![]() .
.
Тогда искомая сумма равна:
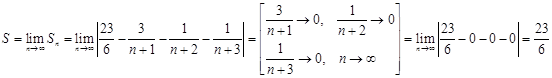
Ответ: ![]() .
.
3. Исследовать ряд на сходимость
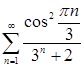
Решение.
Так как ![]() , то рассмотрим ряд
, то рассмотрим ряд
![]() , тогда
, тогда
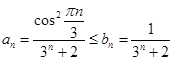
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
