Нестандартные методы решения задач по математике

Следовательно, для доказательства неравенства достаточно показать, что или , где .

Пусть . Для доказате

льства неравенства требуется показать, что , где .

Так как , то корни уравнения являются точками, подозрительными на экстремум функции . Уравнение имеет два корня: , . Поскольку , , , то .

Отсюда следует, что неравенство доказано.

Пример 13 Доказать, если , то

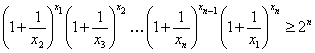
Доказательство. Для получения нижней оценки левой части требуемого неравенства первоначально воспользуемся неравенством Бернулли , а затем неравенством Коши , тогда

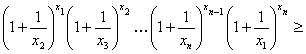
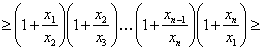
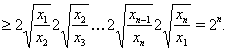
Пример 14 Решить уравнение

Решение. Используя неравенство Коши , можно записать

т.е. имеет место неравенство

Отсюда и из уравнения следует, что приведенные выше неравенства Коши обращаются в равенства. А это возможно лишь в том случае, когда и .

Следовательно, имеем и .

Ответ: , ; , ; , ; , .

Пример 15 Решить уравнение

Решение. Применим к левой части уравнения неравенство Бернулли , а к правой части --- неравенство , тогда

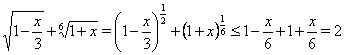
и

Отсюда следует, что неравенства Бернулли, примененные к обеим частям уравнения , обращаются в равенство, а это возможно лишь в том случае, когда .

Ответ: .

Пример 16 Доказать неравенство

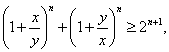
где , .

Доказательство. Непосредственно из неравенства следует . Используя это неравенство и неравенство Коши , получаем неравенство следующим образом:

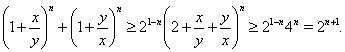
Пример 17 Доказать, что

где , , --- стороны треугольника, a --- его площадь.

Доказательство. Известно, что , где --- угол между сторонами и . Поскольку , то . Используя неравенство Коши , получаем верхнюю оценку площади треугольника вида . По аналогии с изложенным выше имеет место и .

Тогда .

Отсюда следует справедливость неравенства .

Пример 18 Доказать, что для всякого прямоугольного параллелепипеда с ребрами , , и диагональю имеет место неравенство

Доказательство. Воспользуемся неравенством Коши--Буняковского , тогда .

 Скачать реферат