Нестандартные методы решения задач по математике

Таким образом, получено ложное неравенство, которое доказывает справедливость исходного неравенства .

8. Методы, основанные на использовании ограниченности функций

Одним из эффективных методов решения уравнений или неравенств является метод, основанный на использовании ограниченности функций. К наиболее известным ограниченным функциям относятся, например, неко

торые тригонометрические функции; обратные тригонометрические функции; функции, содержащие модуль, степень, корень с четной степенью и т.д.

Приведем наиболее распространенные неравенства. Известно, что , , , , , , , , , , , и многие другие. Здесь --- натуральное число, , и .

Кроме приведенных выше простейших неравенств имеются и более сложные, в частности, тригонометрические неравенства , и неравенства с модулями вида .

Следует также отметить, что при решении некоторых задач, приведенных в настоящем разделе, можно эффективно применять неравенства Коши, Бернулли и Коши--Буняковского, описанные в разделе .

Задачи и решения

Пример 49 Решить уравнение

Решение. Выделим полный квадрат в правой части уравнения, т.е. . Отсюда следует, что . Так как при этом , то из получаем систему уравнений

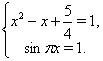
Решением второго уравнения системы является . Подстановкой в первое уравнение убеждаемся, что найденное значение является решением системы уравнений и уравнения .

Ответ: .

Пример 50 Решить уравнение

Решение. Обозначим , тогда из определения обратной тригонометрической функции имеем и .

Так как , то из уравнения следует неравенство , т.е. . Поскольку и , то и . Однако и поэтому .

Если и , то . Так как ранее было установлено, что , то .

Ответ: , .

Пример 51 Решить уравнение

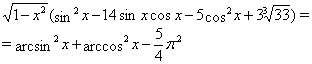
Решение. Областью допустимых значений уравнения являются .

Первоначально покажем, что функция при любых может принимать только положительные значения.

Представим функцию следующим образом: .

Поскольку , то имеет место , т.е. .

Следовательно, для доказательства неравенства , необходимо показать, что . С этой целью возведем в куб обе части данного неравенства, тогда

Полученное численное неравенство свидетельствует о том, что . Если при этом еще учесть, что , то левая часть уравнения неотрицательна.

Рассмотрим теперь правую часть уравнения .

 Скачать реферат