Нестандартные методы решения задач по математике

Ответ: , .

3. Методы, основанные на применении численных неравенств

Нестандартными методами в математике являются также методы, в основу которых положено использование известных в математике численных неравенств (Коши,

Бернулли и Коши--Буняковского), изучению которых в общеобразовательной школе не уделяется или почти не уделяется никакого внимания. Однако многие математические задачи (особенно задачи повышенной сложности) эффективно решаются именно такими методами. В этой связи незнание последних может существенно ограничить круг успешно решаемых задач.

Первоначально приведем формулировки неравенства Коши, неравенства Бернулли и неравенства Коши--Буняковского, а затем проиллюстрируем их применение на примерах, взятых из программы вступительных экзаменов по письменной математике в Белгосуниверситете.

Неравенство Коши

Пусть , , ., , тогда

где . Причем неравенство превращается в равенство тогда и только тогда, когда . В частности, если в положить , то

Это неравенство чаще всего встречается при решении школьных задач по математике. Если в положить и , где , то

Здесь неравенство равносильно равенству лишь при .

Следует отметить, что имеется аналог неравенства для отрицательных значений , а именно, если , то

Данное неравенство превращается в равенство при .

Неравенство Бернулли

Наиболее распространенным является классическое неравенство Бернулли, которое формулируется в следующей форме: если , то для любого натурального имеет место

Причем равенство в достигается при или .

Наряду с существует обобщенное неравенство Бернулли, которое содержит в себе два неравенства:

если или , то

если , то

где .

Следует отметить, что равенства в и имеют место только при . Верно также и обратное утверждение.

Неравенство Коши--Буняковского

Для произвольных и имеет место

где .

Причем равенство в достигается в том и только в том случае, когда числа . и пропорциональны, т.е. существует константа такая, что для всех выполняется равенство .

На основе использования неравенства Коши--Буняковского можно доказать неравенство

которое справедливо для произвольных , и натурального числа .

Задачи и решения

Пример 11 Доказать неравенство

где .

Доказательство. Преобразуем левую часть неравенства с использованием неравенства , т.е.

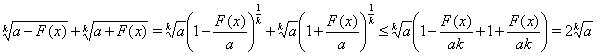
Так как по условию , то равенства в неравенстве Бернулли не будет, поэтому доказано строгое неравенство .

Пример 12 Доказать, что если , то

Доказательство. Введем обозначения и . Тогда и .

Используя неравенство Коши-Буняковского , можно записать . Так как , то и .

Имеет место равенство , из которого следует .

 Скачать реферат