Операции на графах

Операции на графах позволяют образовывать новые графы из нескольких более простых. В этом параграфе будут рассмотрены операции на графах без параллельных ребер (дуг).

Объединение графов.

Пусть G1(X1,E1) и G2(X2,E2) – произвольные графы. Объединением G1ÈG2 графов G1 и G2 называется граф с множеством вершин X1ÈX2, и с множеством ребер (дуг) E1ÈE2.

Рассмот

рим операцию на примере графов G1(X1,E1) и G2(X2,E2), приведенных на рис. 4.1. Множества вершин первого и второго графов соответственно равны X1 = {x1, x2, x3} и X2 = {x2, x3, x4}, а множество вершин результирующего графа определится как X = X1ÈX2 = {x1, x2, x3, x4}. Аналогично определяем множества дуг графа:

E1 = {(x1, x2), (x1, x3), (x2, x1), (x3, x3)}. E2 = {(x2, x4), (x3, x2), (x4, x2)}.

E = {(x1, x2), (x1, x3), (x2, x1), (x3, x3), (x2, x4), (x3, x2), (x4, x2)}.

Результирующий граф G(X,E) = G1(X1,E1)ÈG2(X2,E2) также приведен на рис. 1.

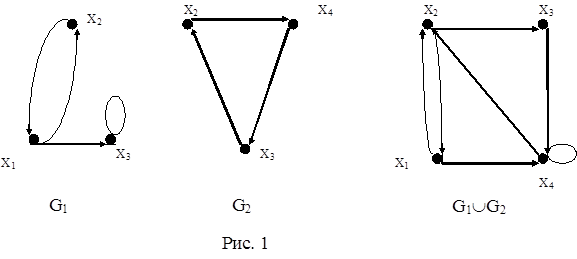
Операция объединения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:

G1ÈG2 = G2ÈG1 – свойство коммутативности;

G1È(G2ÈG3) = (G1ÈG2)ÈG3 – свойство ассоциативности.

Операция объединения графов может быть выполнена в матричной форме. Для графов с одним и тем же множеством вершин справедлива следующая теорема.

Теорема 1. Пусть G1 и G2 – два графа (ориентированные или не ориентированные одновременно) с одним и тем же множеством вершин X, и пусть A1 и A2 – матрицы смежности вершин этих графов. Тогда матрицей смежности вершин графа G1ÈG2 является матрица A = A1ÈA2, образованная поэлементным логическим сложением матриц A1 и A2.

Рассмотрим выполнение операции объединения графов, множества вершин которых не совпадают. Пусть G1(X1,E1) и G2(X2,E2) – графы без параллельных ребер и множества X1 и X2 вершин этих графов не совпадают. Пусть A1 и A2 – матрицы смежности их вершин графов. Для таких графов операция объединения может быть выполнена следующим образом.

В соответствии с определением операции объединения графов найдем множество вершин результирующего графа как X1ÈX2. Построим вспомогательные графы G’1 и G’2, множества вершин которых есть множество X1ÈX2, а множество ребер (дуг) определяется множествами E1 для графа G’1 и E2 для графа G’2. Очевидно, что матрицы A’1 и A’2 смежности вершин этих графов могут быть получены из матриц A1 и A2 путем добавления в них дополнительных столбцов и строк с нулевыми элементами.

Применив к графам G’1 и G’2 теорему 4.1, найдем матрицу смежности вершин графа G’1ÈG’2 как A’1ÈA’2. Очевидно, что полученной матрице смежности вершин соответствует граф, множество вершин которого равно X1ÈX2, а множество ребер определяется, как E1ÈE2, что соответствует операции объединения графов.

Пример 1. Выполнить в матричной форме операцию объединения графов G1 и G2, представленных на рис. 1.

Составим матрицы смежности вершин графов.

Множество вершин результирующего графа X1ÈX2 = {x1, x2, x3, x4}. Составим матрицы смежности вершин вспомогательных графов G’1 и G’2.

 Скачать реферат