Численные методы решения задач условной многомерной оптимизации

Аннотация

Используемые термины: Пусть X и Y — два множества. Закон F, согласно которому каждому элементу поставлен в соответствие единственный элемент, называется отображением множества X в множество Y или функцией, заданной на X со значе

ниями в Y. Экстремум — максимальное или минимальное значение функции на заданном множестве. Задача безусловной оптимизации состоит в нахождении минимума или максимума функции в отсутствие каких-либо ограничений. Условная оптимизация — поиск минимума или максимума функции при наличии ограничений. Безусловная оптимизация — поиск минимума или максимума функции без наличия активных ограничений. Последовательность определенных и неотрицательных функций на множестве называют штрафом или штрафной функцией. Итерационный процесс — многократно повторяющиеся действия (вычисления) до выполнения некоторого условия окончания. Целевая функция – функция, связывающая цель (оптимизируемую переменную) с управляемыми переменными в задаче оптимизации.

В данной работе решается задача поиска экстремума (максимума) функции нескольких переменных при наличии ограничения равенства. Для решения используется метод штрафных функций, который позволяет свести задачу поиска условного экстремума к решению последовательности задач на поиск безусловного экстремума вспомогательной функции.

Оглавление

Введение

1. Основная часть

1.1 Постановка задачи

1.2 Анализ задачи

1.3 Описание метода штрафных функций

1.4 Графическое решение задачи

1.5 Формализация расчетов

2. Структура приложения, предназначенного для решения задачи

3. Результаты вычислений

4. Выводы

5. Список литературы

6. Приложения

Введение

Математическое программирование – математическая дисциплина, изучающая теорию и методы решения задач о нахождении экстремумов функции на множествах конечномерного векторного пространства, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами). В зависимости от природы множеств задачи математического программирования классифицируются как:

· задачи дискретного программирования (или комбинаторной оптимизации) - если множество конечно и счетно;

· задачи целочисленного программирования – если множество является подмножеством множества целых чисел;

· задачи линейного программирования – если все ограничения и целевая функция содержат лишь линейные функции;

· задачи нелинейного программирования – если ограничения или целевая функция содержат нелинейные функции и множество является подмножеством конечномерного векторного пространства.

Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.

Математическое программирование используется при решении оптимизационных задач исследования операций. Способ нахождения экстремума полностью определяется классом поставленной задачи.

В данной работе поставлена задача условной оптимизации, т.е. задача, содержащая некоторые ограничения по независимым переменным на множестве G. Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих равенствам или неравенствам. Ограничения – равенства выражают зависимость между проектными параметрами, которая должна учитываться при нахождении решения. Ограничения-неравенства устанавливают менее жесткие зависимости между проектными параметрами, позволяя им в некоторой части области G оставаться независимыми, а в остальной части проявляется зависимость друг от друга. Решение задачи условной оптимизации зачастую нельзя найти, используя аналитические методы решения, поэтому требуется использование дополнительных численных методов.

В настоящее время разработано множество численных методов для задач как безусловной, так и условной оптимизации.

Методы условной оптимизации, как правило, сводят решение исходной задачи к многократному решению вспомогательной задачи безусловной оптимизации.

Решение безусловной оптимизации является более простым и легко реализуется в современных математических пакетах. Для решения поставленной задачи использовались средства программы MathCAD. Данная программа позволяет выполнить как численные, так и аналитические вычисления, имеет удобный математически-ориентированный интерфейс и прекрасные средства графики. Система MathCAD изначально создавалась для численного решения математических задач, позже в нее были интегрированы инструменты символьной математики из системы Maple, что постепенно превратило MathCAD в универсальный инструмент решения математических задач. Поэтому выбор данного программного средства вполне обоснован.

1. Основая часть

1.1 Постановка задачи

Требуется найти точку такую, что

f( x*) = x1 − 2x22 + 4x2 → max (1)

где (2)

с помощью метода штрафных функций.

1.2 Анализ задачи

Данная задача относится к классу задач нелинейного программирования. Решается методом штрафных функций. Этот метод заключается в сведении задачи, на условный экстремум, к решению последовательности задач на поиск безусловного экстремума вспомогательной функции, которая будет составлена по нижеописанным методам. Решение новой задачи проведем двумя методами безусловной оптимизации разного порядка. Для данного проекта были выбраны метод сопряженных направлений, который является методом нулевого порядка, и метод наискорейшего градиентного спуска, являющийся методом первого порядка.

Недостатком метода наискорейшего спуска является его низкая эффективность в оптимизации овражных функций. Применение данного метода допустимо, так как функция непрерывна на всей области определения (областью определения функции является вся плоскость (x1,x2)), и непрерывны ее частные производные первого порядка:

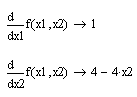
Оба метода безусловной оптимизации сводят задачу поиска наименьшего значения функции нескольких переменных к многократному решению одномерных задач оптимизации. Метод наискорейшего градиентного спуска гарантирует сходимость к точке минимума для сильновыпуклых функций. При уменьшении выпуклости уменьшается и скорость сходимости итерационного процесса. Если требуется найти глобальный минимум функции, то для строго выпуклой функции решение этой задачи аналогично поиску локального минимума. В случае существования нескольких минимумов, поиск глобального минимума сводится к перебору всех локальных минимумов. В методе сопряженных направлений используется тот факт, что минимум квадратичной функции может быть найден не более чем за n шагов при условии, что поиск ведется вдоль сопряженных относительно матрицы Гессе направлений. Так как достаточно большой класс целевых функций может быть представлен в окрестности точки минимума квадратичной аппроксимацией, описанная идея применяется и для неквадратичных функций. Исходная функция является строго выпуклой и, соответственно, имеет только один минимум, что оправдывает выбор методов для поиска безусловного экстремума. Методы безусловной оптимизации можно оценить по следующим параметрам:

 Скачать реферат