Метод наименьших квадратов в случае интегральной и дискретной нормы Гаусса

1. Постановка задачи

При решении многих задач физики и других прикладных наук возникает необходимость вместо функции , рассматривать функцию , представляющую функцию как можно «хорошо».

На

пример: может быть, в частности, и непрерывной функцией на , а соответствующая - алгебраическим или тригонометрическим многочленом, который «достаточно хорошо» приближает функцию .

Например: всякую функцию из можно представить приближённо соответствующим многочленом степени с помощью формулы Тейлора:

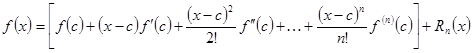(1)

т.е.

; (2)

где , - многочлен степени , приближающий функцию , - остаточный член. Ясно, что

(3)

т.е. - характеризует абсолютную погрешность приближения функции многочленом в точке .

Известно также, что можно приблизить с помощью тригонометрического многочлена – отрезка ряда Фурье.

В утверждение, что функция хорошо приближает функцию на компакте , может быть вложен разный смысл. Например:

а) можно потребовать, чтобы приближающая функция совпадала с в точках промежутка , т.е. выполнялись условия , для .

Если - многочлен степени , то рассматриваемый процесс приближения называется параболическим интерполированием или процессом построения интерполяционного многочлена (частным примером является многочлен Лагранжа, т.е. );

б) функцию можно выбрать так, чтобы норма - отклонения невязки – достигала минимального значения, причём норма может быть определена по-разному, и разным нормам соответствуют различные степени приближения.

В функциональном пространстве Гильберта , норме невязки имеет вид (интегральная норма Гаусса):

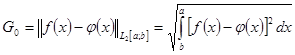(4)

часто, в качестве нормы рассматривают Чебышевскую норму (Т – первая буква фамилии Чебышева на немецком языке):

(5)

При использовании нормы (5) говорят о равномерном приближении функции , функцией .

Подробная теория Т-приближений была развита в работах немецкого математика Л. Коллатца.

На практике, для оценки характера приближения, часто применяют метод наименьших квадратов, при котором невязка вычисляется по дискретной норме Гаусса:

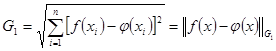(6)

Ясно, что метод наименьших квадратов (6) – является дискретным аналогом функции Гаусса (4).

Принципиальную возможность приближения любой непрерывной функции многочленом даёт теорема Вейерштрасса: Если , тогда , - многочлен, что имеет место неравенство:

(7)

2. Метод наименьших квадратов в случае приближения функции

Мы ранее рассматривали задачу аппроксимации результатов неточного эксперимента линейной функцией . Сейчас рассмотрим общий случай, когда функция приближается некоторой системой линейно независимых функций .

Как известно, для линейной независимости системы функций необходимо и достаточно, чтобы определитель Грама этой системы был отличен от нуля, т.е.

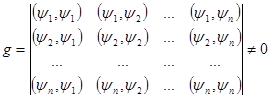(8)

где означают скалярные произведения. Тогда для приближения (аппроксимации) функции применяется линейная комбинация системы базисных функций, т.е.

(9)

В приближающей функции , неизвестными являются коэффициенты разложения , которые подбираются из условия минимума невязки, подсчитываемой по соответствующей норме. Вообще говоря, является элементом линейной оболочки, натянутой на систему базисных функций .

 Скачать реферат