Старший и верхний центральный показатели линейной системы

Содержание

ВВЕДЕНИЕ

1 НЕОБХОДИМЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

2 СООТНОШЕНИЕ

3 СТАРШИЙ И ВЕРХНИЙ ЦЕНТРАЛЬНЫЙ ПОКАЗАТЕЛИ ДЛЯ ДИАГОНАЛЬНОЙ СИСТЕМЫ

3.1 Старший и верхний центральный показатели для диагональной системы с произвольными коэффицие

нтами

3.2 Старший и верхний центральный показатели для диагональной системы с постоянными коэффициентами

4 СТАРШИЙ И ВЕРХНИЙ ЦЕНТРАЛЬНЫЙ ПОКАЗАТЕЛИ НЕКОТОРОЙ ЛИНЕЙНОЙ ОДНОРОДНОЙ ДИАГОНАЛЬНОЙ СИСТЕМЫ. СЛУЧАЙ

4.1 Старший показатель некоторой линейной однородной диагональной системы

4.2 Верхний центральный показатель некоторой линейной однородной диагональной системы

5 ОСНОВНЫЕ СВОЙСТВА ВЕРХНЕГО ЦЕНТРАЛЬНОГО ПОКАЗАТЕЛЯ

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

ВВЕДЕНИЕ

В данной дипломной работе проводится изучение таких понятий, как верхний центральный показатель системы, характеристические показатели Ляпунова; рассматриваются различные соотношения между старшим и верхним центральным показателями линейных систем, то есть рассматриваются случаи, когда старший показатель Ляпунова строго меньше, равен верхнему центральному показателю.

В дипломной работе проводится исследование конкретной линейной однородной диагональной системы: вычисляются характеристические показатели системы, находятся спектр системы, старший показатель системы, а также верхний центральный показатель этой же системы, устанавливается соотношение На конкретном примере выясняется, что роль оценки сверху показателей решений возмущенных систем

играет число , а не .

1. НЕОБХОДИМЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Определение 1.1 [1,с.123]. Наибольший из частичных пределов a функции при называется ее верхним пределом:

.

Определение 1.2 [1,с.125]. Число (или символ или ), определяемое формулой

.

будем называть характеристическим показателем Ляпунова (или характерисическим показателем).

Для показательной функции , очевидно, имеем

.

Лемма 1.1 [1,с.132]. Характеристический показатель конечномерной матрицы совпадает с характеристическим показателем ее нормы, то есть

.

Для вектор-столбца

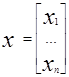
будем использовать одну из норм [1,с.20]:

= ; = ; = .

Свойства характеристического показателя функции [1,с.126,128]:

1) = , ;

2) .

Замечание 1.1 [1,с.130]. Если линейная комбинация функций

, ,

где постоянны, содержит лишь одну функцию с наибольшим характеристическим показателем, то

= .

Определение 1.3 [1,с.142]. Система ненулевых вектор-функций

обладает свойством несжимаемости, если характеристичесий показатель любой существенной их линейной комбинации

, ,

где постоянны, совпадает с наибольшим из характеристических показателей комбинируемых вектор-функций, то есть для всякой комбинации y имеем

= .

Определение 1.4 [1,с.137]. Множество всех собственных характеристических показателей (то есть отличных от и ) решений дифференциальной системы будем называть ее спектром.

Теорема 1.1 [1,с.143]. Фундаментальная система линейной системы

,

где и ─ спектр системы , является нормальной тогда и только тогда, когда она обладает свойством несжимаемости.

Замечание 1.2 [1,с.142]. Совокупность вектор-функций с различными характеристическими показателями, очевидно, обладает свойством несжимаемости.

 Скачать реферат