Определенный интеграл
Содержание
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
2. Геометрический смысл определенного интеграла
3. Основные свойства определенного интеграла
4. Формула Ньютона–Лейбница
5. Замена переменной в определенном интеграле
6. Интегрирование по частям
Лекция 2. Применение определенных интегралов. несобственные интегралы
1. Площад
ь криволинейной трапеции
2. Объем тела вращения
3. Длина дуги плоской кривой
4. Несобственные интегралы с бесконечными пределами интегрирования
5. Несобственные интегралы от неограниченных функций
Литература
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
Пусть функция ![]() определена на отрезке
определена на отрезке ![]() ,
, ![]() . Выполним следующие операции:
. Выполним следующие операции:
1) разобьем отрезок ![]() точками
точками ![]() на n частичных отрезков
на n частичных отрезков ![]() ;
;
2) в каждом из частичных отрезков ![]() ,
, ![]() выберем произвольную точку
выберем произвольную точку ![]() и вычислим значение функции в этой точке:
и вычислим значение функции в этой точке: ![]() ;
;
3) найдем произведения ![]() , где
, где ![]() – длина частичного отрезка
– длина частичного отрезка ![]() ,
, ![]() ;
;
4) составим сумму
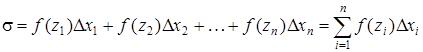 , (1)
, (1)
которая называется интегральной суммой функции y = f(x) на отрезке [а, b]. С геометрической точки зрения интегральная сумма ![]() представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки
представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки ![]() , а высоты равны
, а высоты равны ![]() соответственно (рис. 1). Обозначим через
соответственно (рис. 1). Обозначим через ![]() длину наибольшего частичного отрезка
длину наибольшего частичного отрезка ![]() ;
;
5) найдем предел интегральной суммы, когда ![]() .
.
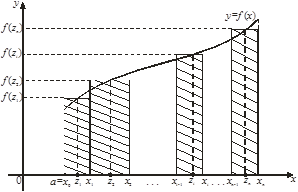
Рис. 1
Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка ![]() на частичные отрезки, ни от выбора точек
на частичные отрезки, ни от выбора точек ![]() в них, то этот предел называется определенным интегралом от функции
в них, то этот предел называется определенным интегралом от функции ![]() на отрезке
на отрезке ![]() и обозначается
и обозначается 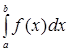 .
.
Таким образом, 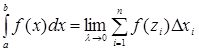 .
.
В этом случае функция ![]() называется интегрируемой на
называется интегрируемой на ![]() . Числа а и b называются соответственно нижним и верхним пределами интегрирования,
. Числа а и b называются соответственно нижним и верхним пределами интегрирования, ![]() – подынтегральной функцией,
– подынтегральной функцией, ![]() – подынтегральным выражением,
– подынтегральным выражением, ![]() – переменной интегрирования; отрезок
– переменной интегрирования; отрезок ![]() называется промежутком интегрирования.
называется промежутком интегрирования.
Теорема 1. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то она интегрируема на этом отрезке.
, то она интегрируема на этом отрезке.
2. Геометрический смысл определенного интеграла
Пусть на отрезке ![]() задана непрерывная неотрицательная функция
задана непрерывная неотрицательная функция ![]() . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, слева и справа – прямыми x = aи x = b(рис. 2).
. Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, слева и справа – прямыми x = aи x = b(рис. 2).

Рис. 2
Определенный интеграл 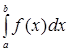 от неотрицательной функции
от неотрицательной функции ![]() с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции
с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции ![]() , слева и справа – отрезками прямых
, слева и справа – отрезками прямых ![]() и
и ![]() , снизу – отрезком
, снизу – отрезком ![]() оси Ох.
оси Ох.
3. Основные свойства определенного интеграла
1. Значение определенного интеграла не зависит от обозначения переменной интегрирования: 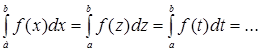 .
.
2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю: 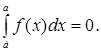
3. Если ![]() , то, по определению, полагаем
, то, по определению, полагаем 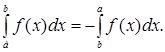
4. Постоянный множитель можно выносить за знак определенного интеграла: 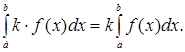
5. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:
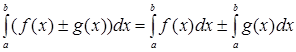 .
.
6. Если функция ![]() интегрируема на
интегрируема на ![]() и
и ![]() , то
, то
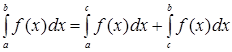 .
.
7. (теорема о среднем). Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то на этом отрезке существует точка
, то на этом отрезке существует точка ![]() , такая, что
, такая, что 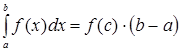 .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
