Несобственные интегралы
1. Несобственные интегралы с бесконечными пределами
При введении понятия определенного интеграла, а также при рассмотрении задач, связанных с ним, все время делалось предположение, что область интегрирования конечна, а интегрируемая функция на нем непрерывна. Если интервал интегрирования бесконечен или функция в этом интервале имеет точки разрыва, то введенное выше понятие определе
нного интеграла неприменимо. Однако существует целый ряд задач, когда возникает необходимость распространить понятие определенного интеграла на случаи бесконечных интервалов интегрирования и разрывных функций.
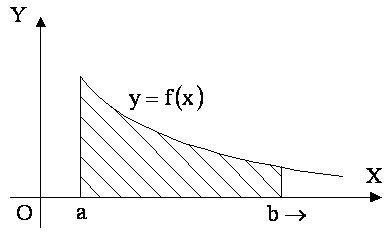
Рассмотрим вначале случай интегралов с бесконечными пределами. Пусть функция ![]() непрерывна на промежутке
непрерывна на промежутке ![]() . Следовательно, можно вычислить любой определенный интеграл с верхним пределом
. Следовательно, можно вычислить любой определенный интеграл с верхним пределом ![]() . Величина этого интеграла будет меняться в процессе изменения
. Величина этого интеграла будет меняться в процессе изменения ![]() , но его можно будет вычислить до тех пор, пока
, но его можно будет вычислить до тех пор, пока ![]() конечное число. Как только верхний предел станет равным бесконечности,
конечное число. Как только верхний предел станет равным бесконечности, ![]() -ая интегральная сумма, приводящая в пределе к определенному интегралу, потеряет смысл. Действительно, в этом случае уже нельзя будет ни задать
-ая интегральная сумма, приводящая в пределе к определенному интегралу, потеряет смысл. Действительно, в этом случае уже нельзя будет ни задать ![]() , ни вычислить
, ни вычислить ![]() . Иначе говоря, последняя частичная трапеция при записи
. Иначе говоря, последняя частичная трапеция при записи ![]() -ой интегральной суммы будет всегда иметь бесконечно большое основание и ее площадь вычислить обычными методами не удастся. В этом случае выход из положения заключается в том, что
-ой интегральной суммы будет всегда иметь бесконечно большое основание и ее площадь вычислить обычными методами не удастся. В этом случае выход из положения заключается в том, что ![]() находится не на бесконечности, а стремится к ней.
находится не на бесконечности, а стремится к ней.
Определение 1. Если существует конечный предел 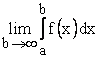 , то этот предел называется несобственным интегралом с бесконечным пределом от функции
, то этот предел называется несобственным интегралом с бесконечным пределом от функции ![]() и обозначается
и обозначается 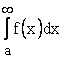 .
.
Итак, по определению  . В этом и заключается метод вычисления таких интегралов. Очевидно, что поскольку данное вычисление связано с нахождением предела, то ответ может существовать или нет.
. В этом и заключается метод вычисления таких интегралов. Очевидно, что поскольку данное вычисление связано с нахождением предела, то ответ может существовать или нет.
Определение 2. Если в несобственном интеграле предел существует, то интеграл называется сходящимся, если предел не существует или равен бесконечности, то интеграл называется расходящимся.
Очевидно, с геометрической точки зрения несобственный интеграл с бесконечными пределами равен площади неограниченной области, лежащей между осью ![]() , кривой
, кривой ![]() и прямой
и прямой ![]() .
.
Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:

Следует подчеркнуть, что интеграл 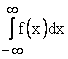 существует только тогда, когда существует каждый из интегралов
существует только тогда, когда существует каждый из интегралов 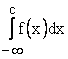 и
и 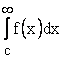 .
.
Из сказанного выше следует, что несобственный интеграл это не предел интегральной суммы, а предел определенного интеграла с переменным верхним пределом интегрирования.
Рассмотрим пример вычисления несобственного интеграла с бесконечным пределом, который, кроме того, применяется и при решении других задач, о чем будет сказано в дальнейшем.
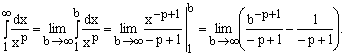
Если ![]() , то
, то ![]() , поэтому
, поэтому 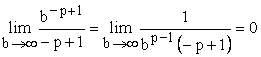 . Следовательно, в этом случае
. Следовательно, в этом случае 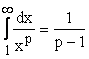 .
.
Если ![]() , то
, то ![]() , поэтому
, поэтому 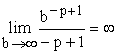 и
и 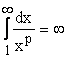 . Аналогично, если
. Аналогично, если ![]() , то
, то 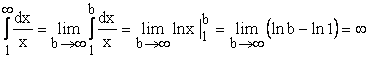 .
.
Таким образом, ![]() сходится, если
сходится, если ![]() и расходится, если
и расходится, если ![]() .
.
Несобственные интегралы с бесконечными пределами имеют место, в частности, в физике при вычислении работы по перемещению материальной точки с массой ![]() из бесконечности в точку
из бесконечности в точку ![]() под действием силы притяжения. Эта работа называется потенциалом силы притяжения материальной точки
под действием силы притяжения. Эта работа называется потенциалом силы притяжения материальной точки ![]() при
при ![]() .
.
2. Несобственные интегралы от разрывных функций
Рассмотрим теперь случай, когда функция ![]() непрерывна на промежутке
непрерывна на промежутке ![]() , а в точке
, а в точке ![]() терпит разрыв второго рода. В этом случае введение определенного интеграла на отрезке
терпит разрыв второго рода. В этом случае введение определенного интеграла на отрезке ![]() как предела интегральной суммы также невозможно. Дело в том, что отрезок
как предела интегральной суммы также невозможно. Дело в том, что отрезок ![]() разбить на
разбить на ![]() частичных отрезков можно, но в этом случае первая частичная трапеция будет иметь бесконечную высоту и ее площадь вычислить невозможно. Однако, как и в случае с бесконечным интервалом интегрирования, здесь также существует выход. Необходимо искать площадь трапеции, левый конец основания которой приближается к точке
частичных отрезков можно, но в этом случае первая частичная трапеция будет иметь бесконечную высоту и ее площадь вычислить невозможно. Однако, как и в случае с бесконечным интервалом интегрирования, здесь также существует выход. Необходимо искать площадь трапеции, левый конец основания которой приближается к точке ![]() .
.
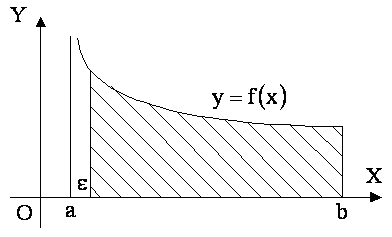
Определение. Если существует конечный предел 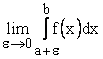 , то этот предел называется несобственным интегралом от разрывной функции
, то этот предел называется несобственным интегралом от разрывной функции ![]() и обозначается
и обозначается 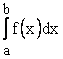 .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
