Непрерывность функции на интервале и на отрезке

Рефераты / Математика / Непрерывность функции на интервале и на отрезке

Определение 3.3 Пусть - некоторая функция, $\mathcal{D}(f)$ - её область определения и $(a;b)\sbs\mathcal{D}(f)$ - некоторый (открытый) интервал (может быть, с 29 src="images/referats/660/image004.gif" alt="$ a=-\infty$">и/или $b=+\infty$ )7. Назовём функцию непрерывной на интервале если непрерывна в любой точке $x_0\in(a;b)$ , то есть для любого $x_0\in(a;b)$ существует $\lim\limits_{x\to x_0}f(x)=f(x_0)$ (в сокращённой записи: $\forall\ x_0\in(a;b)\ \exists\ \lim\limits_{x\to x_0}f(x)=f(x_0)).$

Пусть теперь - (замкнутый) отрезок в $\mathcal{D}(f)$ . Назовём функцию непрерывной на отрезке , если непрерывна на интервале , непрерывна справа в точке и непрерывна слева в точке , то есть $1)\quad\forall\ x_0\in(a;b)\ \exists\ \lim\limits_{x\to x_0}f(x)=f(x_0);$

$2)\quad\exists\ \lim\limits_{x\to a+}f(x)=f(a);$ $3)\quad\exists\ \lim\limits_{x\to b-}f(x)=f(b).$

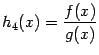Теорема 3.5 Пусть и - функции и - интервал или отрезок, лежащий в $\mathcal{D}(f)\cap\mathcal{D}(g)$ . Пусть и непрерывны на . Тогда функции , , непpеpывны на . Если вдобавок $g(x)\ne0$ пpи всех $x\in I$ , то функция $h_4(x)=\dfrac{f(x)}{g(x)}$ также непpеpывна на .

Из этой теоpемы вытекает следующее утвеpждение, точно так же, как из теоpемы 3.1 - пpедложение 3.3:

Предложение 3.4 Множество $\mathcal{C}_I$ всех функций, непpеpывных на интеpвале или отpезке $I\sbs\mathbb{R}$ - это линейное пpостpанство:

$\displaystyle f_1(x),f_2(x)\in\mathcal{C}_I;C_1,C_2=\mathrm{const}\quad\Longrightarrow \quad C_1f_1(x)+C_2f_2(x)\in\mathcal{C}_I.$

Более сложное свойство непрерывной функции выражает следующая теорема.

Теорема 3.6 (о корне непрерывной функции) Пусть функция непрерывна на отрезке , причём и - числа разных знаков. (Будем для определённости считать, что , а .) Тогда существует хотя бы одно такое значение $x_0\in(a;b)$ , что (то есть существует хотя бы один корень уравнения ).

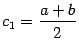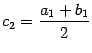Доказательство. Рассмотрим середину отрезка $c_1=\dfrac{a+b}{2}$ . Тогда либо ${f(c_1)=0}$ , либо , либо . В первом случае корень найден: это . В остальных двух случаях рассмотрим ту часть отрезка, на концах которой функция принимает значения разных знаков: в случае или в случае . Выбранную половину отрезка обозначим через и применим к ней ту же процедуру: разделим на две половины и , где $c_2=\dfrac{a_1+b_1}{2}$ , и найдём . В случае корень найден; в случае рассматриваем далее отрезок в случае - отрезок и т.д.