Некоторые вопросы геометрии Лобачевского на модели Пуанкаре
Введение
В развитии геометрии можно указать четыре периода.
Первый период (до 7 в. до н. э) - зарождение геометрии в Египте и Вавилоне. Геометрия этого периода - наука эмпирическая.
Второй период (7-3 в. до н. э) - греческий. В Греции геометрия тесно связана с философией. Геометрия этого периода - наука теоретическая.
В 3 в. до н.э. появились „Начала" Евклида - пер
вая попытка построения геометрии на принципах Аристотеля (384-322 до н. э).
Третий период (17-18 в) развития геометрии связан с переходом её на качественно новую ступень по сравнению с геометрией древних. Этот период времени характерен открытием новых методов исследования и появлением различных дисциплин.
Аналитическая геометрия, дифференциальная геометрия, проективная геометрия, начертательная геометрия - это всё приложения того или иного аппарата к объектам евклидовой геометрии.
Четвёртый период (с 19 в) в развитии геометрии связан с именами русского математика Н.И. Лобачевского (1793-1856), немецкого математика К. Гаусса (1777-1855) и венгерского математика Я. Бойаи (1802-1860).
Именно эти учёные независимо друг от друга пришли к открытию неевклидовой геометрии, которая называется теперь геометрией Лобачевского.
Этот период времени ознаменован более пристальным вниманием математиков к проблеме обоснований геометрии.
Почти в одно и то же время появляются различные аксиоматические системы для обоснования евклидовой геометрии. Одна из них принадлежит немецкому математику Д. Гильберту (1540-1603).
Система аксиом Гильберта состоит из пяти групп (аксиомы связи, аксиомы порядка, аксиомы конгруэнтности, аксиомы непрерывности, аксиома параллельности).
Если в этой системе аксиом заменить аксиому параллельности на аксиому Лобачевского, то мы получим аксиоматику геометрии Лобачевского, которая и рассматривается в дипломной работе.
В связи с аксиоматическим построением геометрии возникает, в частности, вопрос о непротиворечивости выбранной аксиоматики, что связано с построением некоторой модели.
В дипломной работе предлагается одна из моделей геометрии Лобачевского, а именно, модель французского учёного А. Пуанкаре (1854-1912), и с помощью её решается вопрос о непротиворечивости геометрии Лобачевского.
Заметим, что при построении модели Лобачевского большую роль играет инверсия (симметрия относительно окружности). Поэтому первая глава работы посвящена инверсии.
Глава 1. Инверсия и её свойства
1. Определение инверсии
Присоединим к евклидовой плоскости „бесконечно удалённую" точку ![]() . Получим расширенную плоскость, обозначим её через П.
. Получим расширенную плоскость, обозначим её через П.
Пусть в плоскости П дана окружность (O,r) с центром O и радиусом r.
Определение. Инверсией относительно окружности (O,r) называют такое отображение П на себя, при котором всякой точке А![]() П, (А≠О, А≠
П, (А≠О, А≠![]() ) ставится в соответствие точка А'
) ставится в соответствие точка А'![]() П так, что выполняются условия:
П так, что выполняются условия:
1) А'![]() [OA),
[OA),
2) |OA|·|OA'|=![]() .
.
Точке О ставим в соответствие точку ![]() и, обратно, точке
и, обратно, точке ![]() -точку О.
-точку О.
Символом ![]() обозначим инверсию относительно окружности (O,r).
обозначим инверсию относительно окружности (O,r).
Отметим простейшие свойства инверсии, которые вытекают из определения.
![]() . Пусть А
. Пусть А![]() П и
П и ![]() (A) =A'. Тогда
(A) =A'. Тогда ![]() (A') =A.
(A') =A.
Точки А и А' называются инверсными.
![]() . Инверсия является 1-1 отображением расширенной плоскости П на себя.
. Инверсия является 1-1 отображением расширенной плоскости П на себя.
![]() . Пусть А
. Пусть А![]() П и
П и ![]() (A) =A'.
(A) =A'.
Если |OA|>r, то |OA'|<r.
Если |OA|<r, то |OA'|>r.
Если |OA|=r, то |OA'|=r.
Таким образом, точки окружности (O,r) и только они, являются при ![]() неподвижными.
неподвижными.
Легко выполнить построение точки, инверсной данной. Рассмотрим три возможных случая:
1) |OA|=r, то A'=A.
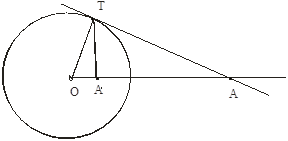
2) |OA|>r. Проведём [OA). Через точку А проводим касательную к (O, r). Пусть Т - точка касания. Проведём из Т перпендикуляр на [OA). Основание этого перпендикуляра и есть искомая точка А'. Действительно, из прямоугольного ![]() ОТА имеем |OA|·|OA'|=
ОТА имеем |OA|·|OA'|=![]() =
=![]() .
.
3) |OA|<r. В силу свойства ![]() получаем
получаем
следующее построение: восставляем в точке А перпендикуляр к [OA), в точке пересечения этого перпендикуляра с (O, r) проводим касательную к (O, r) и в пересечении касательной с [OA) получаем искомую точку А'.
Продолжим рассмотрение свойств инверсии.
![]() . Пусть A
. Пусть A![]() Пи В
Пи В![]() Пи
Пи ![]() (A) =A',
(A) =A',![]() (B) =B'.
(B) =B'.
Тогда
![]()
Доказательство.
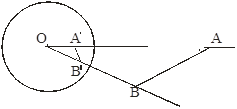
![]() ОАВ~
ОАВ~![]() ОВ'А',
ОВ'А',
тогда
![]() .
.
Учитывая, что
![]() ,
,
получаем
![]()
Введём понятие сложного отношения четырёх точек.
Определение.
![]() .
.
![]() . Инверсия сохраняет сложное отношение четырёх точек.
. Инверсия сохраняет сложное отношение четырёх точек.
Доказательство. Даны точки A, B, C, D. ![]() (A) =A',
(A) =A',
![]() (B) =B',
(B) =B', ![]() (C) =C',
(C) =C', ![]() (D) =D'. Используя предыдущее свойство, имеем:
(D) =D'. Используя предыдущее свойство, имеем:
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
