Числовые характеристики случайной функции и выборочная функция распределения

Контрольная работа №1

Задача 1. Задана случайная функция

где, , .

Найти числовые характеристики =48 height=28 src="images/referats/7443/image005.png">, , .

Решение. Согласно свойству мат. ожидания суммы случайных функций имеем

Математическое ожидание произведения случайной величины на неслучайную функцию равно произведению неслучайной функции на мат. ожидание случайной величины

Дисперсия случайной функции равна

Раскроем квадрат разности

С учетом названных выше свойств мат. ожидания получим

Корреляционная функция случайной функции для моментов времени и определяется по формуле вида

Преобразуем произведение под знаком математического ожидания следующим образом

В результате, корреляционная функция будет определена, как мат. ожидание полученной случайной функции, а именно

Ответ:

Задача 2. Дана спектральная плотность

Определить корреляционную функцию и дисперсию .

Решение. Корреляционная функция определяется как

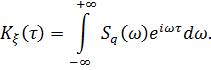
Подставим исходные данные и найдем интеграл

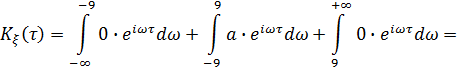
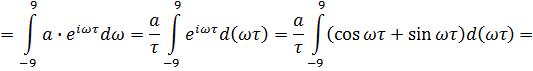
Дисперсия равна

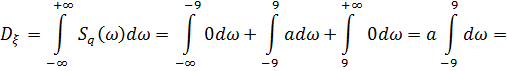
Задача 3. Найти числовые характеристики производной случайной

функции, если

, .

Решение. Так как математическое ожидание производной случайной функции равно производной математического ожидания этой функции, то с учетом исходных данных получим

Корреляционная функция производной случайной функции равна второй смешанной частной производной от ее корреляционной функции. Имеем

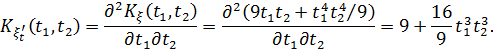
Дисперсия равна

Ответ:

Контрольная работа №2

1. Сгруппировать заданную выборку объема (количество интервалов равно 10).

2. Построить выборочную функцию распределения и гистограмму.

3. Вычислить среднее выборочное и несмещенную выборочную дисперсию .

4. Построить доверительный интервал для .

5. Используя критерий согласия , проверить гипотезу о нормальном распределении.

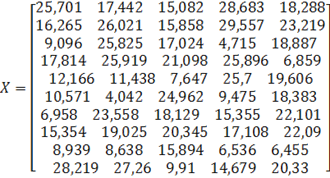
Решение. Упорядочим элементы выборки от минимального значения к максимальному:

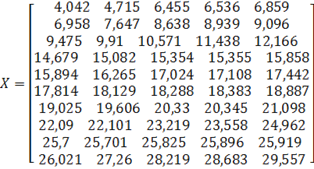
Длина интервала равна

За левую границу первого интервала примем значение . Тогда правая граница последнего (десятого) интервала равна

.

 Скачать реферат