Задачи на экстремум в планиметрии

Введение

Развитие логического мышления, которое осуществляется на занятиях алгеброй и геометрией, оказывает серьёзное влияние на изучение любых наук. Знания, умения и навыки, приобретаемые при изучении этих предметов, важны для трудовой и профессиональной подготовки. Обучение алгебре и геометрии способствует формированию диалектико–материалистического мировоззрения, с

одействует умственному развитию, в процессе которого вырабатываются умения обобщать и конкретизировать, систематизировать и классифицировать, проводить анализ и синтез, осуществлять самоконтроль. В процессе обучения формируются и такие личностные качества, как точность и ясность словесного выражения мысли, сосредоточенность и внимание, настойчивость, ответственность и трудолюбие. На мой взгляд, геометрия в этом деле хорошая помощница.

Итак, геометрия – это раздел математики, изучающий пространственные отношения и формы, а планиметрия – это часть геометрии, изучающая фигуры на плоскости. Моя курсовая работа на задачи на экстремум в планиметрии. Обратимся к определению экстремума - наибольшее или наименьшее значение функции. Ещё задолго до того, как сформировались общие понятия переменной величины и функции, они фактически использовались в математике. Значительную роль в развитии этих понятий сыграл метод координат, созданный французским математиком П. Ферма (1601-1665) и Р. Декартом (1596-1650). Метод координат стал широко использоваться для графического исследования функции и графического решения уравнений. С этого времени начался новый этап, который ознаменовался мощным развитием не только математики, но и всего естествознания.

Термин «функция» (от лат. Functio-исполнение, совершение) ввёл немецкий математик Г. Лейбниц (1646-1716). У него функция связывалась с графиком.

У Л. Эйлера появился и более общий подход к понятию функции как зависимости одной переменной величины от другой. Эта точка зрения получила дальнейшее развитие в трудах Н.И. Лобачевского, П. Дирихле и других учёных. Что же такое экстремум в планиметрии? В своей курсовой работе я постараюсь найти ответ на этот вопрос.

§ 1. Максимум и минимум

Определение. Говорят, что функция f(x) имеет максимум в точке х = а, если в достаточной близости от этой точки всем значениям х (как большим, так и меньшим а) соответствуют значения меньшие, чем f(a).

Функция f(x) имеет минимум в точке х = а,если в достаточной близости от этой точки всем значениям х соответствуют значения f(x), большие, чем f(а).

Короче: функция f(x) имеет максимум (минимум) в точке х = а, если значение f (а) больше (меньше) всех соседних значений. Максимум и минимум объединяются

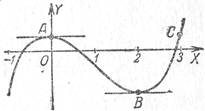
Рис. 1 наименованием экстремум 2).

Пример. Функция f(x) = ⅓ х3 - х2 + ⅓ (рис. 1) имеет максимум в точке х = 0 [точка А (0; ⅓) выше всех соседних] и минимум в точке х = 2 [точка В (2; -1) ниже всех соседних].

1) Предполагается, что функция дифференцируема в промежутке (а, b).

2) Латинское слово «экстремум» означает «крайнее».

Замечание. В обыденной речи выражения «максимум» и «наибольшая величина» равнозначны. В анализе термин «максимум» имеет более узкий смысл. Именно максимум функции может и не быть ее наибольшим значением. Так, функция f(x) = ⅓ х3 - х2 + ⅓

(см. рис. 1), рассматриваемая, скажем, в промежутке (— 1; 4), имеет в точке х = 0 максимум, ибо вблизи от этой точки [а именно в промежутке (— 1; 3)] всем значениям х соответствуют значения f(x), меньшие, чем f (0), т. е. чем ⅓ (в указанном промежутке график расположен ниже точки А). Тем не менее максимум f (0) не является наибольшим значением функции в промежутке (— 1; 4), ибо при х > 3 имеем:

f(x) > ⅓

(справа от С график расположен выше точки А). Однако разыскание наибольшего значения функции в данном промежутке тесно связано с разысканием ее максимумов (см.§ 6). Аналогичное замечание для минимума.

§ 2. Необходимое условие максимума и минимума

Теорема. Если функция f (х) имеет экстремум (т. е. максимум или минимум) в точке х = а, то в этой точке производная либо равна нулю, либо бесконечна, либо не существует.

Г е о м е т р и ч е с к и: если график имеет в точке А максимальную ординату, то в этой точке касательная либо горизонтальна (рис. 1), либо вертикальна (рис. 2), либо не существует (рис. 3). То же для минимальной ординаты (точка В на рис. 1, точка А на рис. 4, точки В и С на рис. 3).

Замечание. Условие экстремума, высказанное в теореме, необходимо, но не достаточно, т. е. производная в точке х = а может обращаться в нуль (рис. 5), в бесконечность (рис. 6) или не существовать (рис. 7) без того, чтобы функция имела экстремум в этой точке.

§ 3. Первое достаточное условие максимума и минимума

Теорема. Если в достаточной близости от точки х = а производная f '(х) положительна слева от а и отрицательна справа от а (рис. 8), то в самой точке х = а функция f(x) имеет максимум при условии, что функция f(x) здесь непрерывна 1).

Если, наоборот, слева от а производная f(х) отрицательна, а справа положительна (рис. 9), то f (х) имеет в точке а минимум при условии, что она здесь непрерывна 2).

Теорема выражает тот факт, что f(x) при переходе от возрастания к убыванию имеет максимум, а при переходе от убывания к возрастанию — минимум.

1) Однако, f(x) может и не быть дифференцируемой при х = а (см. рис. 2).

2) Однако, f(x) может и не быть дифференцируемой при х = а

З а м е ч а н и е. Согласно теореме признаком экстремума функции f(x) является перемена знака производной f '(х) при прохождении аргумента через рассматриваемое значение х = а.

Если же при прохождении через х = а производная сохраняет знак, то f(x) возрастает в точке х = а, когда производная положительна как справа, так и слева от х = а(рис. 5, 6, 7), и убывает, когда производная отрицательна (рис. 10).[Снова предполагается, что f(x) непрерывна при х = а.]

§ 4. Правило разыскания максимумов и минимумов

Пусть функция f(x) дифференцируема в промежутке (а, b). Чтобы найти все ее максимумы и минимумы в этом промежутке, надо:

1) Решить уравнение f '(х) = 0 (корни этого уравнения называются критическими значениями аргумента; среди них надо будет искать значения х, дающие экстремум функции f(x); см. § 2).

2) Для каждого критического значения х = а исследовать, меняет ли знак производная f(x) при переходе аргумента через это значение. Если f '(х) переходит от положительных значений к отрицательным (при переходе от х < а к х > а), то имеем максимум (§ 3), если от отрицательных значений к положительным, то минимум.

Если же f ' (х) сохраняет знак, то нет ни максимума, ни минимума: при f '(х) > 0 функция f(х) в точке а возрастает, при f '(х) < 0 убывает (§ 3, замечание).

Замечание 1. Если функция f(x) непрерывна в промежутке (а, b), но в отдельных его точках не дифференцируема, то эти точки надо причислить к критическим и произвести аналогичное исследование.

 Скачать реферат