Линейные дифференциальные уравнения

Содержание

Введение

1. Линейные системы

1.1 Предварительные определения и обозначения

1.2 Линейные однородные системы

1.3 Неоднородные линейные системы

1.4 Линейные системы с постоянными коэффициентами

1.5 Линейные системы с периодическими коэффициентами

2. Линейные дифференциальные уравнения

2.1 Линейные дифференциальные уравнения порядка n

2.2 Линейны

е уравнения с аналитическими коэффициентами

2.3 Асимптотическое поведение решений некоторых линейных систем

3. Решение задач

Заключение

Список литературы

Введение

При изучении физических явлений часто не удается непосредственно найти законы, связывающие физические величины, но сравнительно легко устанавливается зависимость между теми же величинами, их производными или дифференциалами.

Таким образом, большинство физических явлений описывается на языке дифференциальных уравнений, содержащих неизвестные функции под знаком производной или дифференциала.

В работе рассматриваются понятия простейших дифференциальных уравнений, а также линейных дифференциальных уравнений произвольного порядка и систем таких уравнений. Особое внимание уделяется изучению линейных дифференциальных уравнений с постоянными коэффициентами и систем линейных уравнений.

Решением дифференциального уравнения называется n раз дифференцируемая функция , удовлетворяющая уравнению во всех точках своей области определения.

Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительные условие: например, потребовать, чтобы решение принимало в данной точке данное значение.

Задача нахождения решения обыкновенного дифференциального уравнения или системы обыкновенных дифференциальных уравнений, удовлетворяющего некоторым начальным условиям, называется задачей Коши.

Основные задачи и результаты теории дифференциальных уравнений: существование и единственность решения различных задач для обыкновенных дифференциальных уравнений, методы решения простейших обыкновенных дифференциальных уравнений , качественное исследование решений обыкновенных дифференциальных уравнений без нахождения их явного вида.

Цель дипломной работы – изучить понятие линейных дифференциальных уравнений.

В связи с поставленной целью необходимо выполнить следующие задачи:

1) Рассмотреть понятие линейных систем;

2) Изучить линейные дифференциальные уравнения различных порядков, в том числе с аналитическими коэффициентами;

3) Решить предложенные практические задания.

1. Линейные системы

1.1 Предварительные определения и обозначения

Пусть А = (aij) – квадратная матрица порядка n, где aij – комплексные числа. Определим норму А следующим образом:

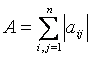. (1.1)

Если n-мерный вектор х представлять как матрицу с n строками и одним столбцом, то норма вектора совпадает с нормой x, определенной по формуле (1). Легко видеть, что норма обладает следующими свойствами:

(I) |A+B| |A|+|B|,

(II) |AB| |A|*|B|,

(III) |Ax| |A|*|x|,

где А и В – матрицы, х – n-мерный вектор.

По определению, расстояние между двумя матрицами А и В равно |A-B|, и это расстояние удовлетворяет обычным свойствам метрики.

Нулевая матрица будет обозначаться через О, единичная – через Е. В случае опасности смешения размерностей эти квадратные матрицы порядка n будут обозначаться соответственно через Оn и Еn.

Заметим, что | Оn | = 0 и | Еn | = n, а не 1.

Комплексно сопряженной матрицей для А = (aij) называется матрица , где - комплексно сопряженные числа для aij. Транспонированная матрица обозначается через и определяется так: . Сопряженная матрица для А определяется так: . Заметим, что |A*|=||=||=|A|. Далее, (АВ)*=В*А*. Определитель матрицы А обозначается как det А.

Если det А = 0, то матрица А называется особой. Не особая матрица имеет обратную матрицу А-1, которая удовлетворяет соотношениям

А А-1 = А-1А = Е.

Многочлен det (λЕ-А) степени n от λ называется характеристическим многочленом для матрицы А, а его корни – характеристическими корнями А. Если эти корни обозначены λi (i = 1, …, n), то

det (λЕ-А) =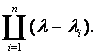

Две квадратные матрицы А и В порядка n называются подобными, если существует Неособая квадратная матрица Р порядка n, такая что

В = РАР-1.

Если А и В подобны, то они имеют один и тот же характеристический многочлен, ибо

det (λЕ-В) = det (Р(λЕ-А)Р-1)= det Р* det (λЕ-А)* det Р-1= det (λЕ-А).

В частности, коэффициенты многочлена det (λЕ-А) при степенях λ инвариантны относительно преобразования подобия. Два наиболее важных инварианта - det А и sp A – определитель и след А соответственно.

Приведем следующий фундаментальный результат о канонической форме матрицы.

Теорема 1.1 Каждая квадратная матрица А порядка n и подобная матрица вида

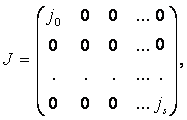
где J0 – диагональная матрица с элементами λ1, λ2,…, λq и

(i = 1, …, s).

Здесь λj , j = 1, …, q+s, - характеристические корни А, не обязательно различные. Если λj – простой корень, то он встречается в J0 и поэтому, если все корни различны, А подобна диагональной матрице

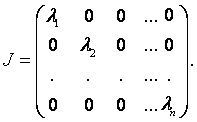
Из теоремы 1.1 непосредственно следует, что

det А = , sp A =

где произведение и сумма распространены на все корни, причем каждый корень считается столько раз, каков а его кратность. Матрицы Ji имеют вид

Ji = λq+iЕri+Zi ,

где Ji – квадратная матрица порядка ri и

Матрицы Ji можно представить также в виде λq+iЕri+γZi, где γ – любая постоянная, отличная от нуля.

 Скачать реферат