Линейные дифференциальные уравнения

Доказательство проводится по индукции. Для n = 1 А = - а1; значит det(λE1 - A) = λ + а1 и, следовательно, (6.19) верно для n = 1. Предположим, что результат справедлив для n – 1. Разложим определитель

det(λEn - A) =

по элементам первого столбца и заметим, что коэффициент при λ есть определител

ь (n-1)-го порядка, именно det(λEn-1 – A1), где

Поэтому λdet(λEn-1 – A1) = λn + а1 λn-1 +…+ аn--1λ. Единственный другой ненулевой элемент в первом столбце есть аn и его алгебраическое дополнение равно 1. Поэтому det(λEn – A) = λn + а1 λn-1 +…+ аn--1λ + аn, что и требовалось доказать.

Теорема 6.5 (без доказательства). Пусть λ1, …, λn - различные корни характеристического уравнения

f(λ) = λn + а1 λn-1 +…+ аn = 0

и пусть кратность корня λi равна mi (i = 1, …, s ). Тогда фундаментальное множество для (6.16) дается n функциями

tkeλi (k = 0, 1,…, mi – 1; i = 1, 2,…, s). (6.20)

2.2 Линейные уравнения с аналитическими коэффициентами

Предположим, что А – квадратная матрица порядка n и b – n-мерный вектор, определенные и аналитические в односвязной области D z-плоскости, и пусть . Используя метод последовательных приближений, нетрудно показать, что линейная система

(7.1)

при условии

имеет в D единственное аналитическое решение .

В самом деле, пусть и пусть С – дуга длины L, лежащая в D, соединяющая точки z0 и z1 и имеющая непрерывно вращающуюся касательную. Обозначим через s длину дуги вдоль С, начиная от точки z0. Выберем постоянную К настолько большой, чтобы было | A(z) | < K и || < K для . Пусть и

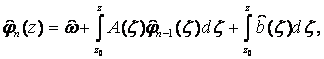
причем интеграл берется вдоль С, так что приближения определены на С. Нетрудно получить оценки

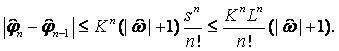
Очевидно, эти оценки справедливы для всех точек z в D, достижимых из z0 другой длины L, на которой |A(z)| и || ограничены постоянной K. Отсюда следует, что эти оценки справедливы в каждом фиксированном множестве R, содержащемся в D. Так как каждая функция аналитична в R, то из равномерной сходимости следует, что предельная функция также аналитична в R. Далее,

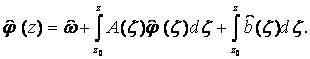
Это доказывает утверждение для R и, следовательно, для D.

Кроме того, все теоремы, доказанные в пп. 1.2 и 1.3, будучи существенно алгебраической природы, справедливы для системы (7.1).

Соответственно этому, если n+1 функций а1, …, аn, b аналитичны в D, то линейное уравнение порядка n

(7.2)

имеет в D единственное решение, удовлетворяющее условиям

, , …, ,

где w1, …, wn – n данных комплексных чисел. Наконец, все результаты п. 2.1 распространяются очевидным образом на случай (7.2).

2.3 Асимптотическое поведение решений некоторых линейных систем

Если коэффициенты линейной системы дифференциальных уравнений при стремятся к постоянным, то иногда возможно охарактеризовать поведение решений.

Здесь рассматривается проблема для действительного переменного. Рассмотрим пример

где v – действительная дифференцируемая функция, для которой , r – интегрируемая функция и

,

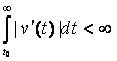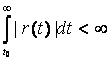
для некоторого t0. (На самом деле достаточно, чтобы функция v имела в интервале ограниченную вариацию.) Без ограничения общности можно в дальнейшем предполагать, что t0 = 0. Из доказанной ниже теоремы следует, что рассматриваемое уравнение имеет два решения φ и ψ, такие, что

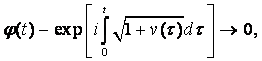
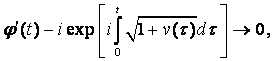
при , а ψ имеет аналогичное поведение с заменой i на –i.

Этот результат показывает, что функция r нисколько не влияет на грубую асимптотику. Однако случай

(0 < α < 1)

убеждает нас в том, что влияние v существенно. Эти асимптотические формулы показывают также, что если положить в уравнении функцию r(t) равной нулю, а 1 + v(t) – постоянной, то результат будет отличаться от точного только членом о(1) при .

В дальнейшем будет рассматриваться линейная система

(8.1)

которая включает как частный случай предыдущий пример.

Теорема 8.1. Пусть А – постоянная матрица с различными характеристическими корнями μj, j = 1, …, n. Пусть матрица V дифференцируема и удовлетворяет условию

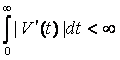(8.2)

и пусть при . Пусть матрица R интегрируема и

 Скачать реферат