Линейные дифференциальные уравнения
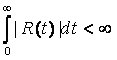 . (8.3)
. (8.3)
Обозначим корни уравнения det (A + V(t) - λE) = 0 через λj(t), j = 1, …, n. Очевидно, что можно, если это необходимо, переставить μj так, чтобы ![]() . Для каждого k положим
. Для каждого k положим
![]()
Допустим, что все j, 1![]() j
j ![]() n, попадают в один из двух классов I1 и I2, где
n, попадают в один из двух классов I1 и I2, где
![]() , если
, если 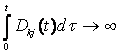 при
при ![]()
и
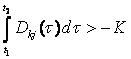
![]() , (8.4)
, (8.4)
![]() , если
, если 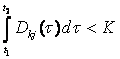
![]() ; (8.5)
; (8.5)
здесь k фиксировано и К – постоянная. Пусть pk – характеристический вектор А, соответствующий μk, так что
Аpk = μk pk. (8.6)
Тогда существует решение φk системы (8.1) и число t0, 0 ![]() t0
t0 ![]()
![]() , такие, что
, такие, что
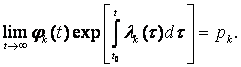 (8.7)
(8.7)
Доказательство. Если условия теоремы выполняются для всех k, 1 ![]() k
k ![]() n, и Ф – матрица со столбцами φ1, …, φn, то Ф – фундаментальная матрица, так как det Ф(t)
n, и Ф – матрица со столбцами φ1, …, φn, то Ф – фундаментальная матрица, так как det Ф(t) ![]() 0 для больших t, ибо pk линейно независимы.
0 для больших t, ибо pk линейно независимы.
Предположим в начале, что А + V(t) для t ![]() t0 имеет диагональный вид А(t) причем t0 выбрано так, что
t0 имеет диагональный вид А(t) причем t0 выбрано так, что
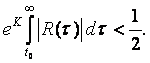 (8.8)
(8.8)
Пусть Ψ(t) – диагональная матрица:
Ψ(t) = 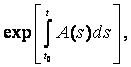
так что
![]() (8.9)
(8.9)
Пусть еК - вектор-столбец со всеми нулевыми элементами, за исключением k-го, который равен 1, и ψk – вектор, определенный равенством
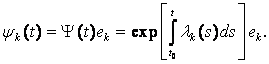
При фиксированном k и I1, I2, определенных согласно неравенствам (8.4), (8.5), положим
Ψ = Ψ1 + Ψ2,
где диагональные матрицы Ψ1 и Ψ2 содержат элементы Ψ, соответствующие столбцам с индексами j, принадлежащим соответственно I1 и I2. Тогда
![]() (j = 1, 2). (8.10)
(j = 1, 2). (8.10)
Рассмотрим теперь уравнение
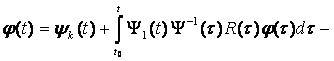
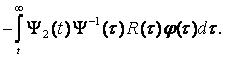 (8.11)
(8.11)
Можно непосредственно проверить, что если уравнение (8.11) имеет решение φ, то
![]() = (A + R) φ. (8.12)
= (A + R) φ. (8.12)
Последнее уравнение имеет рассматриваемый нами вид (8.1)
Пусть φ0(t) = 0 и
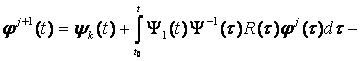
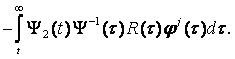 (8.13)
(8.13)
Тогда φ1(t) = ψk(t) и для t ![]() t0
t0
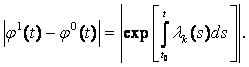 (8.14)
(8.14)
Каждый элемент диагональной матрицы ![]() имеет вид
имеет вид
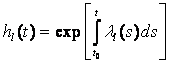
![]()
или равен нулю. Но для t0 ![]() τ
τ![]() t
t
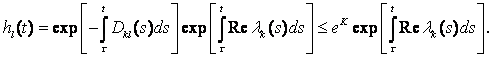
Поэтому для t0 ![]() τ
τ![]() t
t
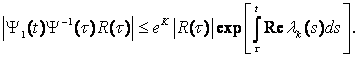
Точно также для τ ![]() t получим
t получим
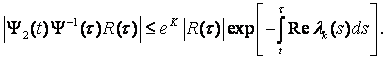
Используя эти неравенства, получаем из (8.13)
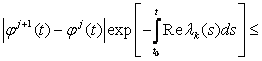
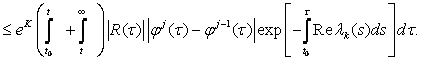
Из (8.8) и (8.14) теперь по индукции следует
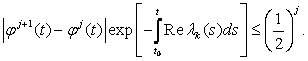
Отсюда следует равномерная сходимость последовательности {φj} на каждом конечном подинтервале интервала [t0,![]() ). Так как φj непрерывно, то предельная функция φ также непрерывна и, очевидно,
). Так как φj непрерывно, то предельная функция φ также непрерывна и, очевидно,
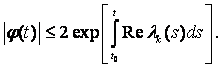 (8.15)
(8.15)
Покажем теперь, что
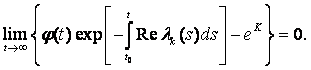 (8.16)
(8.16)
Это будет установлено, если мы покажем, что при t→ ∞
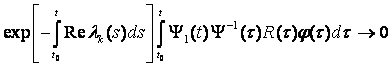 (8.17)
(8.17)
И
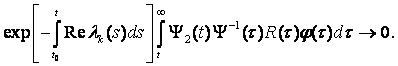 (8.18)
(8.18)
Доказательство соотношения (8.18) сразу получается из (8.15) и (8.5). Доказательство соотношения (8.17) основывается на равенстве
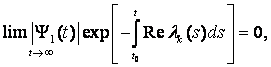 (8.19)
(8.19)
которое является следствием (8.4). Каково бы ни было ε > 0, можно подобрать такое t1, что
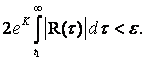
Поэтому, обозначая левую часть (8.17) через J(t), получаем
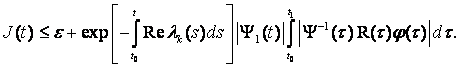
Из (8.19) следует, что
![]()
Так как ε произвольно, то (8.17) доказано. Таким образом, теорема доказана для случая A + V(t) = A(t), если за φ взята φk.
Доказательство теоремы 8.1 вытекает из следующей леммы.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
