Линейные дифференциальные уравнения
det (ФС)=( det Ф)( det С) ![]() 0,
0,
то ФС – фундаментальная матрица.
Наоборот, если Ф1 и Ф2 – две фундаментальные матрицы , то Ф2 = Ф1С, где С – некоторая постоянная неособая матрица. Для доказательства этого положим Ф1-1Ф2 = Ψ(t). Тогда Ф2 = Ф1Ψ. Дифференцируя это равенство, получим, что height=36 src="images/referats/643/image068.gif">. Отсюда и из (2.1) следует, что
![]() , или
, или ![]() . Поэтому
. Поэтому ![]() и, следовательно, матрица ψ = С постоянна. Она неособая, так как этим свойством обладают Ф1 и Ф2.
и, следовательно, матрица ψ = С постоянна. Она неособая, так как этим свойством обладают Ф1 и Ф2.
Замечания. Если предполагать, что Ф2 – решение, то матрица С может быть особой.
Заметим, что если Ф – фундаментальная матрица системы (ЛО) и С – постоянная неособая матрица, то СФ, вообще говоря, не является фундаментальной матрицей.
Две различные однородные системы не могут иметь одну и ту же фундаментальную матрицу, ибо из уравнения (ЛО) следует, что ![]() Поэтому матрица Ф определяет матрицу А однозначно, хотя обратное утверждение и неверно.
Поэтому матрица Ф определяет матрицу А однозначно, хотя обратное утверждение и неверно.
Сопряженные системы. Если Ф - фундаментальная матрица для системы (ЛО), то
![]()
или, переходя к сопряженным матрицам,
![]()
Поэтому ![]() - фундаментальная матрица для сопряженной системы (ЛО) и матричное уравнение
- фундаментальная матрица для сопряженной системы (ЛО) и матричное уравнение
![]()
![]() . (2.3)
. (2.3)
Система (2.3) называется сопряженной для системы (ЛО) и матричное уравнение
![]()
![]() (2.4)
(2.4)
называется сопряженным для уравнения (2.2.). Это соответствие симметрично, ибо (ЛО) и (2.2) сопряжены (2.3) и (2.4) соответственно.
Теорема 2.4. Если Ф - фундаментальная матрица для системы (ЛО), то Ψ есть фундаментальная матрица для сопряженной системы (2.3) в том и только в том случае, когда
![]() (2.5)
(2.5)
где С – постоянная неособая матрица.
Доказательство. Если Ф - фундаментальная матрица для системы (ЛО) и Ψ есть фундаментальная матрица системы (2.3), то так как ![]() - фундаментальная матрица частного вида уравнения (2.3),
- фундаментальная матрица частного вида уравнения (2.3),
![]()
где D – некоторая постоянная неособая матрица (теорема 2.3). Поэтому
![]()
и можно принять С = D*.
Наоборот, если Ф - фундаментальная матрица для сопряженной системы (ЛО) и удовлетворяет (2.5), то ![]() или
или ![]() и, следовательно, в силу теоремы 2.3 Ψ - фундаментальная матрица сопряженной системы (2.3).
и, следовательно, в силу теоремы 2.3 Ψ - фундаментальная матрица сопряженной системы (2.3).
Если А = - А*, то ![]() , будучи фундаментальной матрицей для системы (2.3), является также фундаментальной матрицей для системы (ЛО). Поэтому в силу теоремы 2.3
, будучи фундаментальной матрицей для системы (2.3), является также фундаментальной матрицей для системы (ЛО). Поэтому в силу теоремы 2.3 ![]() или
или
![]() (2.6)
(2.6)
где С – постоянная неособая матрица. Из уравнения (2.6), в частности, следует, что эвклидова длина каждого вектора-решения системы (ЛО) постоянна.
Понижение порядка однородной системы. Если известно m (0<m<n) линейно зависимых решений системы (ЛО), то можно понизить порядок системы на m единиц, и следовательно, дело сведется к решению линейной системы порядка n-m.
Предположим, что φ1 , φ2 , …, φm - m линейно независимых векторов, которые являются решениями системы (ЛО) на интервале I. Пусть вектор φj имеет компоненты φij (i = 1, …, n). Тогда ранг прямоугольной матрицы с элементами φij (i = 1, …, n; j = 1, …, m) для каждого ![]() равен m, так как ее столбцы линейно независимы. Это означает, что для каждого
равен m, так как ее столбцы линейно независимы. Это означает, что для каждого ![]() в этой матрице найдется отличный от нуля определитель порядка m. Выберем некоторое
в этой матрице найдется отличный от нуля определитель порядка m. Выберем некоторое ![]() и предположим для определенности, что в точке t0 отличен от нуля определитель матрицы Фm с элементами φij (i = 1, …, m; j = 1, …, m). Тогда в силу непрерывной зависимости определителя от его элементов φij и непрерывности функций φij в окрестности t0 получим, что det Фm(t)
и предположим для определенности, что в точке t0 отличен от нуля определитель матрицы Фm с элементами φij (i = 1, …, m; j = 1, …, m). Тогда в силу непрерывной зависимости определителя от его элементов φij и непрерывности функций φij в окрестности t0 получим, что det Фm(t) ![]() 0 для t из некоторого интервала
0 для t из некоторого интервала ![]() , содержащего t0. Пусть
, содержащего t0. Пусть ![]() - один из таких интервалов; процесс понижения проведем для
- один из таких интервалов; процесс понижения проведем для ![]() . (Идея этого процесса является модификацией метода вариации произвольных постоянных.)
. (Идея этого процесса является модификацией метода вариации произвольных постоянных.)
Пусть матрица U имеет своими первыми m столбцами векторы φ1 , φ2 , …, φm и своими n-m столбцами – векторы еm+1, …, en, где ej – вектор-столбец со всеми нулевыми элементами, кроме j-го, который равен 1. Очевидно, что U – неособая матрица на ![]() . Сделаем в (ЛО) подстановку
. Сделаем в (ЛО) подстановку
x = Uy. (2.7)
Заметим, что решениям х = φj (j = 1, …, m) при подстановке (2.7) соответствуют решения y = ej (j = 1, …, m). Поэтому подстановку (2.7) можно рассматривать как систему относительно y, которая должна иметь решения ej (j = 1, …, m).
Подставляя (2.7) в систему (ЛО), получаем
![]()
или в координатах,
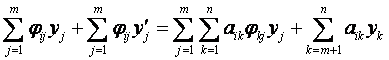 (i = 1, …, m),
(i = 1, …, m),
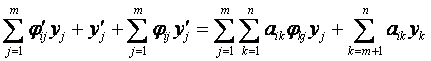 (i = m+1, …, n).
(i = m+1, …, n).
Выражая то обстоятельство, что векторы φj с компонентами φij являются решениями системы (ЛО), получаем
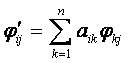 (i = 1, …, n; j = 1, …, m),
(i = 1, …, n; j = 1, …, m),
откуда следует, что
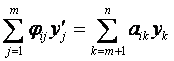 (i = 1, …, m),
(i = 1, …, m),
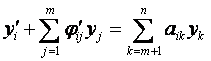 (i = m+1, …, n). (2.8)
(i = m+1, …, n). (2.8)
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
