Линейные дифференциальные уравнения

Так как каждый вектор-решение задачи (6.1), (6.2) есть линейная комбинация n линейно независимых векторов-решений, то каждое решение уравнения есть линейная комбинация n линейно независимых решений этого уравнения. Это доказывает теорему.

Ввиду свойства, указанного в теореме 6.1, множество n линейно независимых решений

уравнения называется базисом или фундаментальным множеством для уравнения .

Теорема 6.2. Пусть φ1, …, φn - n функций, имеющих на интервале I непрерывные производные порядка n, и пусть W(φ1, …, φn)(t) 0 на I. Тогда существует единственное однородное дифференциальное уравнение порядка n (с коэффициентом при х(n), равным единице), для которого эти функции образуют фундаментальное множество, а именно:

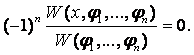(6.6)

Замечание. Вронскиан W(х, φ1, …, φn) представляет собой определитель матрицы, первая строка которой состоит из элементов х, φ1, …, φn, а последующие строки являются последовательными производными первой строки до порядка n включительно.

Доказательство. Очевидно, что W(φi, φ1, …, φn) = 0 (i = 1, …, n), ибо в этом определителе имеются два одинаковых столбца. Разложение числителя W(х, φ1, …, φn) левой части уравнения (6.6) по элементам первого столбца показывает, что (6.6) есть дифференциальное уравнение порядка n. Коэффициент при х(n) в W(х, φ1, …, φn) равен (-1)n W(φ1, …, φn), т.е. в (6.6) при х(n) равен единице. Так как W(φ1, …, φn) 0, то из теоремы 6.1 следует, что φ1, …, φn образуют для (6.6) фундаментальное множество.

Единственность уравнения (6.6) следует из того, что соответствующие векторы с компонентами определяют матрицу коэффициентов (6.2), соответствующие системе (6.1), однозначно. Так имеется взаимно однозначное соответствие между линейными уравнениями порядка n и линейными системами вида (6.1), (6.2), то доказательство завершено.

Если одно или более из решений уравнения известно, то использование соответствующей системы (6.1) позволяет понизить порядок уравнения. Более прямо достигает цели следующий процесс, который является методом вариации постоянных применительно к уравнению . Пусть и положим х = уφ1. Тогда уравнение является для у линейным дифференциальным уравнением порядка n, которое имеет решение у = 1, ибо φ1 есть решение уравнения . Поэтому в новом уравнении коэффициент при у должен обращаться в нуль. Рассматривая это уравнение относительно переменной u = , получим уравнение (n-1)-го порядка. Если φ2 не зависит от φ1 и , то есть решение (n-1)-го порядка для u, которое может быть аналогично сведено к уравнению (n-2)-го порядка, и т.д.

Сопряженные уравнения. С формальным оператором Ln тесно связан другой линейный оператор порядка n, называемый сопряженным для Ln и определяемый следующим образом:

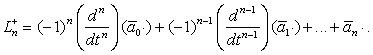
Иначе говоря, если g – функция на I, для которой произведение (k = 0, 1, …, n) имеет n – k производных на I, то

Уравнение

(в подробной записи

),

называемое сопряженным для Lnх = 0 на I, определяется как задача отыскания функции φ (решения), на I, такой, что произведение (k = 0, 1, …, n) имеет n – k производных на I,удовлетворяющей на I уравнению

Если на I и φ – решение уравнения, имеющее n производных на I, то, используя правило дифференцирования произведения, получаем

разделив на , видим, что φ есть решение дифференциального уравнения порядка n рассмотренного выше типа.

Рассмотрим тот специальный случай оператора Lnх когда а0 = 1. Для системы (6.1), (6.2), ассоциированной с уравнением

(6.7)

сопряженная система имеет вид

, (6.8)

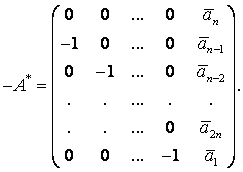
где в силу (6.2)

(6.9)

Записывая (6.8) в компонентах, получаем в силу (6.9)

(k = 2, …, n). (6.10)

Таким образом, если φ1, …, φn – решение системы (6.10), для которого и

существуют, то дифференцируя k-е равенство (6.10) k-1 раз и решая относительно, получаем

Поэтому φn удовлетворяет уравнению

которое является сопряженным к (6.7).

Важность оператора обуславливается интересным соотношением, связывающим Ln и и совершенно необходимым при изучении краевых задач.

 Скачать реферат