Линейные дифференциальные уравнения

Нулевая вектор-функция на I является решением системы (ЛО). Это решение называется тривиальным. Если решение системы (ЛО) равно нулю для некоторого , то в силу теоремы единственности оно равно нулю тождественно на I.

Теорема 2.1. Множество всех решений системы (ЛО) на интервале I образует n-мерное векторное пространство

над полем комплексных чисел.

Доказательство. Если φ1 и φ2 – решения (ЛО) и с1 , с2 – комплексные числа, то с1φ1 + с2φ2 также является решением (ЛО). Это показывает, что решения образуют векторное пространство.

Чтобы доказать, что это пространство n-мерно, следует показать, что существует n линейно зависимых решений φ1 , φ2 , …, φn , таких, что каждое другое решение системы (ЛО) есть линейная комбинация (с комплексными коэффициентами) этих φi . Пусть ξi , i=1, 2, …, n – линейно независимые векторы n-мерного х-пространства. Например, за ξi можно взять вектор со всеми компонентами, равными нулю, кроме i-й, которая равна 1. Тогда, по теореме существования, если , то существуют решения φi, i=1, 2, …, n, системы (ЛО), для которых φi(τ) = ξi . Покажем, что эти решения удовлетворяют поставленному выше условию.

Если бы решения φi были линейно зависимы, то существовали бы n комплексных чисел , не равных одновременно нулю и таких, что

.

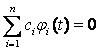
Отсюда следует равенство

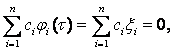
противоречащее предположению о том, что векторы ξi линейно независимы.

Если φ – некоторое решение (ЛО) на I, такое, что φ(τ)=ξ , то можно найти (единственным образом определенные) постоянные сi , удовлетворяющие равенству

,

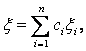ибо векторы ξi образуют базис n-мерного х-пространства. Поэтому функция

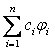
есть решение (ЛО), принимающее при t = τ значение ξ, и, следовательно, в силу теоремы единственности

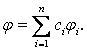
Итак, каждое решение φ есть (единственная) линейная комбинация φi и теорема 2.1 полностью доказана.

Всякое множество φ1 , φ2 , …, φn линейно зависимых решений системы (ЛО) называется базисом или фундаментальным множеством решений системы (ЛО).

Если Ф – матрица, n столбцов которой являются n линейно независимыми решениями (ЛО) на I, то Ф называется фундаментальной матрицей системы (ЛО). Очевидно, Ф удовлетворяет матричному уравнению

. (2.1)

Под матричным дифференциальным уравнением, соответствующим системе (ЛО) на I, подразумевается задача отыскания квадратной матрицы Ф порядка n, столбцы которой являются решениями системы (ЛО) на I. Эта задача обозначается так:

. (2.2)

Матрица Ф называется решением задачи (2.2) на I, и Ф удовлетворяет уравнению (2.1). Из теоремы 2.1. следует, что зная фундаментальную матрицу системы (ЛО), которая является, разумеется, частным решением уравнения (2.2), мы будем знать полную систему решений системы (ЛО).

Теорема 2.2. Для того, чтобы решение-матрица уравнения (2.2) была фундаментальной матрицей, необходимо и достаточно, чтобы det Ф(t) 0 для .

Замечание. Если det Ф(t) 0 для некоторого , то в силу (1.8) det Ф(t) 0 для всех t.

Доказательство теоремы 2.2. Пусть Ф – фундаментальная матрица, столбцами которой являются векторы φj , и пусть φ – некоторое нетривиальное решение системы (ЛО). В силу теоремы 2.1 существуют единственным образом определенные постоянные с1 , с2 , …, сn , не равные все нулю и такие, что

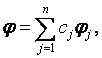
или, выражая при помощи матрицы Ф,

где с – вектор-столбец с элементами с1 , с2 , …, сn . Это соотношение при каждом есть система n линейных уравнений с неизвестными с1 , с2 , …, сn , имеющая единственное решение для каждого φ(τ). Поэтому det Ф(τ) 0 и, по сделанному выше замечанию, det Ф(t) 0 для каждого . Заметим, что это доказывает линейную независимость векторов-столбцов фундаментальной матрицы для каждого .

Наоборот, пусть Ф – матрица-решение уравнения (2.2) и пусть det Ф(t) 0 для каждого . Таким образом, векторы-столбцы матрицы Ф линейно независимы для каждого .

Матрица из векторов-столбцов может иметь определитель, тождественно равный нулю на интервале I, даже при линейно независимых векторах.

Например, пусть

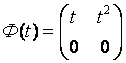
для каждого действительного интервала I. Содержание теоремы 2.2 состоит в том, что этого не может случиться для векторов, которые являются решениями системы (ЛО).

Теорема 2.3. Если Ф – фундаментальная матрица для системы (ЛО) и С – (комплексная) постоянная неособая матрица, то ФС также является фундаментальной матрицей системы (ЛО). Каждая фундаментальная матрица системы (ЛО) может быть представлена в такой форме при помощи некоторой неособой матрицы С.

Доказательство. Из (2.1), если Ф – фундаментальная матрица, вытекает, что

,

Или

и, следовательно, ФС есть матрица-решение уравнения (2.2). Так как

 Скачать реферат