Линейные дифференциальные уравнения

,

.

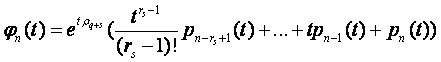В этих формулах р1 , р2 , …, рn - периодические векторы-столбцы матрицы Р1.

Из (5.10) очевидно, что если Reρi < 0 или, что эквивалентно, | λi | < 1, то при решения φi(t) экспоненциально убывают.

Из (5.6) следует, что Ф(ω) = Ф(0)еωR, и поэтому λi можно рассматривать как характеристические корни матрицы Ф-1(0)Ф(ω). В частности, если Ф(0) = Е, то еωR = Ф(ω) и λi являются характеристическими корнями матрицы Ф(ω). Так как

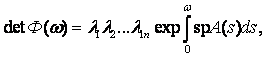(5.11)

то n-й корень можно определить из (5.11), если известны n-1 корней λi.

Действительная неособая матрица С не обязана иметь действительный логарифм, т.е. не всегда существует действительная матрица В, такая что еВ = С. В самом деле, матрица с одной строкой и одним столбцом С = -1 доставляет соответствующий пример. Однако справедливо утверждение, что для действительной матрицы С существует действительная матрица В, такая, что С2 = еВ .

Используя это при доказательстве теоремы 5.1, нетрудно получить следующий результат6 если в системе (5.1) матрица А (t) действительная периодическая с периодом ω, то каждой действительной фундаментальной матрице Ф соответствует действительная матрица Р периода 2ω и действительная постоянная матрица R, такие, что

Ф(t) = Р(t)еtR.

2. Линейные дифференциальные уравнения

2.1 Линейные дифференциальные уравнения порядка n

Предположим, что n+1 коэффициентов а0, а1, …, аn представляют собой непрерывные (комплексные) функции, определенные на действительном t-интервале I, и пусть Ln обозначает формальный дифференциальный оператор

;

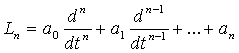это означает, что если функция g имеет n производных на I, то

Далее предположим, что а0(t) 0 для . Тогда, по определению, уравнение

(в подробной записи ()) есть дифференциальное уравнение

;

оно называется линейным однородным дифференциальным уравнением порядка n. Соответствующая этому уравнению система есть векторное уравнение

(6.1)

где

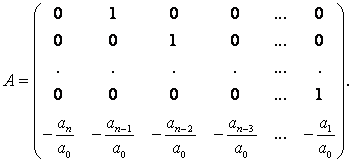(6.2)

Так как (6.1) – линейная система с непрерывной на I матрицей коэффициентов А, то существует единственный вектор-решение φ на I системы (6.1), удовлетворяющий условию

где , |ξ| < . Таким образом, φ1 – первая компонента - удовлетворяет условиям

…, (6.3)

Так как φ1 – решение уравнения , то это решение удовлетворяет условиям (6.3).

Применим теперь остальные результаты, полученные ранее для линейных систем, к уравнению .

Если φ1, …, φn – n решений уравнения , то матрица

(6.4)

есть матрица-решение для (6.1). Определитель этой матрицы называется вронскианом уравнения , соответствующим решениям φ1, …, φn, и обозначается через W(φ1, …, φn). При фиксированных φ1, …, φn он является функцией t на I и его значение в точке t обозначается W(φ1, …, φn)(t). Из того, что для линейной системы вида (6.1)

,

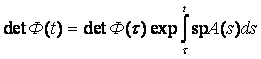
следует (замечая из (6.2), что spA = - а1/а0)

W(φ1, …, φn)(t) = W(φ1, …, φn)(τ)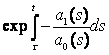 . (6.5)

Теорема 6.1. Необходимое и достаточное условие того, чтобы n решений φ1, …, φn уравнения на интервале I были линейно независимы, заключается в том, что

W(φ1, …, φn) 0 .

Каждое решение уравнения есть линейная комбинация с комплексными коэффициентами любых n линейно независимых решений.

Доказательство. Если решения φ1, …, φn на I линейно зависимы. То существуют постоянные с1, …, сn, не все равные нулю, такие, что

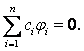
Отсюда следует тождество

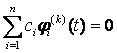(k = 0, 1, …, n-1),

и поэтому векторы с компонентами (i = 1, 2, …, n) линейно зависимы на I. Наоборот, если векторы линейно зависимы, то тем же свойством обладают решения φ1, …, φn уравнения. Из теоремы 2.2 следует, что необходимое и достаточное условие линейной независимости векторов заключается в том, что det Ф(t) 0 на I, где Ф – матрица (6.4). Но это требование в точности совпадает с условием W(φ1, …, φn)(t) 0 на I. В силу (6.5), если W(φ1, …, φn)(τ) 0 для некоторого , то W(φ1, …, φn)(t) 0 для любого .

 Скачать реферат