Преобразование Лапласа

Введение

Преобразование Лапласа — интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинала). С его помощью исследуются свойств

а динамических систем и решаются дифференциальные и интегральные уравнения.

Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями.

1. Прямое преобразование Лапласа

Преобразованием Лапласа функции действительной переменной , называется функция комплексной переменной , такая что:

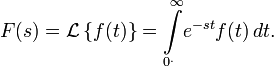
Правая часть этого выражения называется интегралом Лапласа.

2. Обратное преобразование Лапласа

Обратным преобразованием Лапласа функции комплексного переменного , называется функция действительного переменного, такая что:

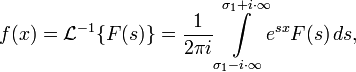
где — некоторое вещественное число. Правая часть этого выражения называется интегралом Бромвича.

3. Двустороннее преобразование Лапласа

Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции участвуют значения x < 0

Двустороннее преобразование Лапласа определяется следующим образом:

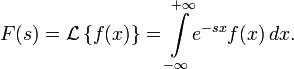
4. Дискретное преобразование Лапласа

Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций. Различают -преобразование и -преобразование.

· -преобразование

Пусть

решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени , где — целое число, а — период дискретизации. Тогда применяя преобразование Лапласа получим:

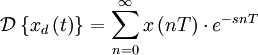
· -преобразование

Если применить следующую замену переменных:

получим Z-преобразование:

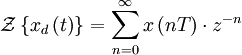
5. Свойства и теоремы

· Абсолютная сходимость

Если интеграл Лапласа абсолютно сходится при σ = σ0, то есть существует предел

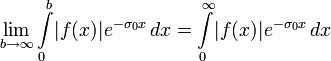
то он сходится абсолютно и равномерно для и F(s) — аналитическая функция при ( — действительная часть комплексной переменной s). Точная нижняя грань σa множества чисел σ, при которых это условие выполняется, называется абсциссой абсолютной сходимости преобразования Лапласа для функции f(x).

· Условия существования прямого преобразования Лапласа

Преобразование Лапласа существует в смысле абсолютной сходимости в следующих случаях:

1. Случай : преобразование Лапласа существует, если существует интеграл

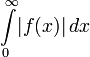
2. Случай σ > σa: преобразование Лапласа существует, если интеграл

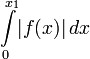
существует для каждого конечного

x1 > 0 и для

3. Случай σ > 0 или σ > σa (какая из границ больше): преобразование Лапласа существует, если существует преобразование Лапласа для функции f'(x) (производная к f(x)) для σ > σa.

Примечание: это достаточные условия существования.

 Скачать реферат