Интегральное исчисление
Задание. Найти неопределенные интегралы. Результат проверить дифференцированием.
а)
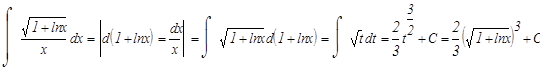
Используемый прием интегрирования называется подведением под знак дифференциала. Проверим результат дифференцированием.
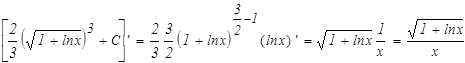
б)
В этом интеграле также используе
тся подведение под знак дифференциала
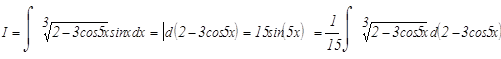
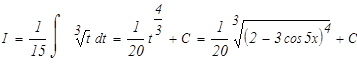
Проверим результат дифференцированием.
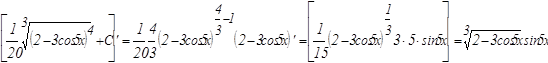
в)
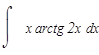
Для решения этого интеграла воспользуемся формулой интегрирования "по частям". Приведем формулу интегрирования по частям:
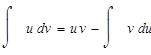
В этом интеграле распишем составляющие следующим образом:
![]()
![]()
Продифференцируем u и проинтегрируем dv чтобы мы могли применить формулу интегрирования по частям:
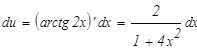
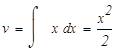
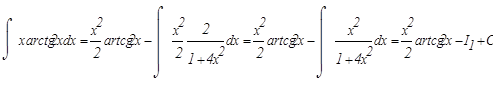
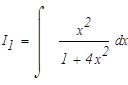
Подинтегральное выражение есть неправильная рациональная дробь. Необходимо привести ее к сумме правильных рациональных дробей, выполнив деление углом числитель на знаменатель.
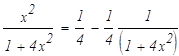
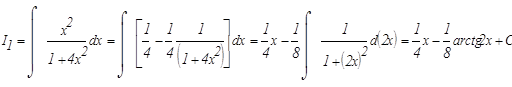
Вернемся к исходному интегралу:
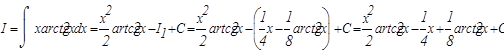
Проверим результат дифференцированием:
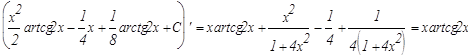
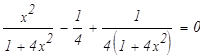
г)
интеграл дифференцирование уравнение парабола
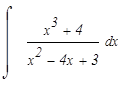
Подинтегральное выражение является неправильной рациональной дробью. Необходимо преобразовать ее в сумму правильных рациональных дробей, выполнив деление углом числитель на знаменатель:
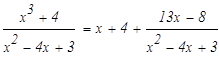
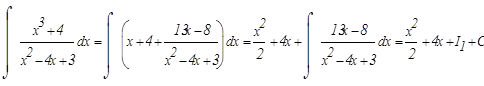
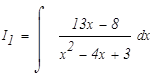
Подинтегральное выражение представляет собой правильную рациональную дробь. Чтобы проинтегрировать её необходимо её представить в виде суммы простейших дробей. Найдем корни знаменателя
![]()
по теореме Виета
![]()
![]()
![]()
Разложим правильную рациональную дробь в сумму простейших методом неопределенных коэффициентов:
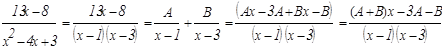
Приравнивая коэффициенты при одинаковых степенях х, составим систему линейных алгебраических уравнений для определения неизвестных коэффициентов А и В:
![]()
![]()
![]()
Решая СЛАУ находим значения коэффициентов:
![]()
![]()
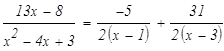
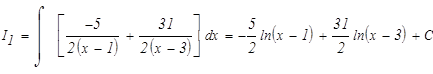
Возвратимся к исходному интегралу:
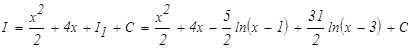
Результат проверим дифференцированием:
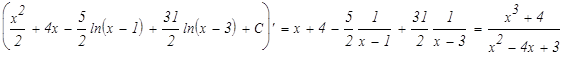
Задание. Вычислить по формуле Ньютона-Лейбница определенный интеграл.
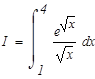
Перейдем к замене переменных в определенном интеграле:
![]()
![]()
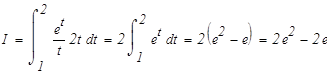
Задание. Вычислить площадь фигуры, ограниченной параболой ![]() и прямой
и прямой ![]() . Сделать чертеж.
. Сделать чертеж.
Решение. Площадь области S, ограниченной снизу функцией g(x), сверху- функцией f(x), слева - вертикальной прямой ![]() , справа - вертикальной прямой равна
, справа - вертикальной прямой равна ![]() равна определенному интегралу:
равна определенному интегралу:
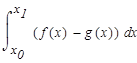
Так как мы пока не знаем, какая же из функций является большей на отрезке ![]() , построим чертеж. Точки
, построим чертеж. Точки ![]() ,
, ![]() являются абсциссами точек пересечения графиков этих двух функций.
являются абсциссами точек пересечения графиков этих двух функций.

Как видно из построения парабола лежит выше прямой на отрезке, поэтому:
![]()
![]()
Абсциссы точек пересечения суть соответственно -6 и -1. Эти значения мы также можем получить решив в системе уравнения двух кривых
![]()
![]()
![]()
![]()
![]()
по теореме Виета имеем: ![]() ,
, ![]() . Теперь осталось только применить формулу вычисления площади криволинейной области:
. Теперь осталось только применить формулу вычисления площади криволинейной области:
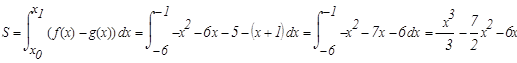
|
|
Другие рефераты на тему «Математика»:
- Прогнозирование функций по методу наименьших квадратов
- Теория вероятностей и математическая статистика
- Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца
- Статистический анализ условий социально-экономического развития Ленинградской области
- Решение военно-логистических задач по выбору оптимального маршрута для военно-транспортных средств
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
