Алгебра октав

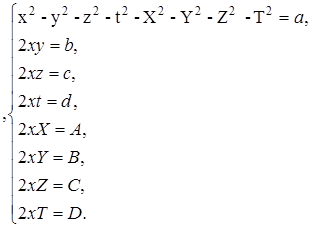
Если x ≠ 0, тo из первого уравнения системы следует, что

4х4 - 4ах2 – (b2 + c2 + d2 + A2 + B2 + C2 + D2) = 0

x2= (a± mg width=264 height=27 src="images/referats/3160/image108.png">) = (a± |w|).

Так как х2 ≥ 0, то х2 = (a± |w|), откуда x=± .Определив х, значения y, z, t, X, Y, Z, T находим из равенств

y = , z = , t = , X = , Y = , Z = , T = .

Из рассмотрения свойств кватернионов и октав можно заметить, что у этих числовых систем много общего. Алгебраические формы записи элементов этих числовых систем представляют собой некоторые многочлены от действительного числа и мнимых единиц с действительными коэффициентами. Одинаковым образом вводится понятие элемента сопряженного данному элементу. Свойства сопряженных элементов одни и те же, в некоторых случаях лишь с поправкой на число мнимых единиц. Понятие модуля кватерниона и октавы вводится одинаковым образом и обладает одинаковыми свойствами. То, что квадрат чисто мнимого кватерниона или октавы есть неположительное действительное число, дает для них возможность записи в виде а + t, где а R и t2 ≤ 0. Формула извлечения корня квадратного как из кватерниона, так и из октавы одна и та же, опять-таки с учетом количества мнимых единиц. При внимательном подходе к аксиоматическому определлллению этих числовых систем так же можно заметить общий подход к построению моделей этих числовых систем. Это так называемый метод удвоения, который заключается в том, что при введении нового числового множества мы строим декартов квадрат предыдущего чисссслового множества и новые числа рассматриваем как упорядоченные пары из чисел предыдущего числового множества. Так, удвоением множества действительных чисел получили множество комплексных чисел, удвоением множества комплексных-чисел - множество кватернионов, удвоением множества кватернионов - множество октав, причем операции сложения и умножения в построенных моделях определялись совершенно одинаково. Такими же свойствами обладает и множество комплексных чисел, однако, в силу того, что их. свойства хорошо изучены на младших курсах, здесь ограничились лишь аксиоматическим построением этой числовой системы.

Теорема Фробениуса, которую мы рассмотрели в , поле комплексных чисел и тело кватернионов анализирует с общей точки зрения, как частные случаи ассоциативной линейной алгебры с делением и содержащей единицу. В дальнейшим мы попытаемся установить общий подход к таким числовым системам, как поле комплексных чисел, тело кватернионов и алгебра октав.

4.2 Алгебраическое сопряжение

Определение. Алгебраическим сопряжением называется сопряжение, которое в сочетании с операцией умножения позволяет в любой алгебре получать действительное число. Как видим, различий относительно сопряжения по мнимой единице два - во-первых, отсутствует требование использования операции сложения и во-вторых в сочетании с произведением требуется получение числа именно алгебры действительных чисел, а не одной из предшествующих удвоению.

.

Или, алгебраическое сопряжение используется для определения модуля числа алгебры.

Для того, чтобы получить действительное число в случае произвольной гиперкомплексной алгебры, следует придумать процедуру, с помощью которой можно отбросить все мнимые единицы. Наиболее простой операцией сопряжения, при этом похожей на определенное выше сопряжение, является операция смены знаков сразу у всех мнимых единиц числа, безотносительно способа их получения и их свойств:

.

Сменив знаки при всех мнимых единицах, получим:

.

Естественно, что столь вольное обращение с мнимыми единицами не может гарантировать, что является действительным числом. Но при этом отметим, что сумма как раз является действительным числом. Таким образом, нам нужно отображение, которое произведению в одной области сопоставляет сложение в другой и наоборот. Такой операцией является пара отображений - логарифмирование и потенцирование. Еще раз напомним их свойства:

,

,

в случае, если a и b коммутируют по умножению.

Таким образом, для получения числа, алгебраически сопряженного заданному, нужно найти его логарифм, сменить знаки у всех мнимых единиц и потенцировать.

Любое число любой гиперкомплексной алгебры естественным образом коммутирует как само с собой, так и с действительным числом, поэтому

.

Или, если

, то .

Среди свойств алгебраического сопряжения отметим весьма важные:

- сопряженное произведения равно обратному произведению сопряженных:

,

,

- в некоторых алгебрах алгебраическое сопряжение совпадает по результату с сопряжением по действительных чисел, все виды сопряжения в ней совпадают. Сопряжение по мнимой единице:

.

a) Алгебраическое сопряжение:

;

,

то есть смена знаков мнимых единиц после логарифмирования эквивалентна смене знака у мнимой единицы самого числа:

.

Здесь одинаково обозначены сопряжение по мнимой единице и алгебраическое. Полагаю, пока нет совмещения сопряжений в одной формуле, разночтений возникнуть не должно.

 Скачать реферат