Дифференциальное исчисление функций
Содержание
1. Введение в анализ и дифференциальное исчисление функции одного переменного
2. Дифференциальное исчисление функций и его приложение
3. Интегральное исчисление функции одного переменного
1. Введение в анализ и дифференциальное исчисление функции одного переменного
1. Вычислить предел:  .
.
Решение.
При ![]() имеем
имеем
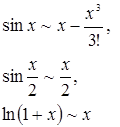
Следовательно,
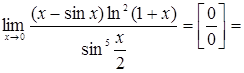
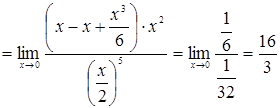
2. Найти асимптоты функции: ![]() .
.
Решение.
Очевидно, что функция не определена при ![]() .
.
Отсюда получаем, что
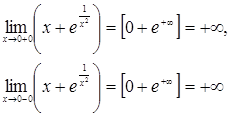
Следовательно, ![]() – вертикальная асимптота.
– вертикальная асимптота.
Теперь найдем наклонные асимптоты.
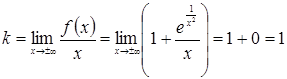
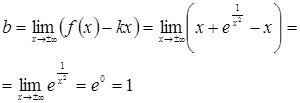
Следовательно, ![]() – наклонная асимптота при
– наклонная асимптота при ![]() .
.
3. Определить глобальные экстремумы: ![]() при
при ![]() .
.
Решение.
Известно, что глобальные экстремумы функции на отрезке достигаются или в критических точках, принадлежащих отрезку, или на концах отрезка. Поэтому сначала находим ![]() .
.
![]() .
.
А затем находим критические точки.
![]()
![]()
![]()
Теперь найдем значение функции на концах отрезка.
![]() .
.
Сравниваем значения и получаем:
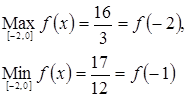
4. Исследовать на монотонность, найти локальные экстремумы и построить эскиз графика функции: ![]() .
.
Решение.
Сначала находим ![]() .
.
![]() .
.
Затем находим критические точки.
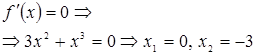
|
x |
|
–3 |
|
0 |
|
|
|
– |
0 |
+ |
0 |
+ |
|
|
убывает |
min |
возрастает |
возрастает |
возрастает |
Отсюда следует, что функция
возрастает при ![]() ,
,
убывает при ![]() .
.
Точка ![]() – локальный минимум.
– локальный минимум.
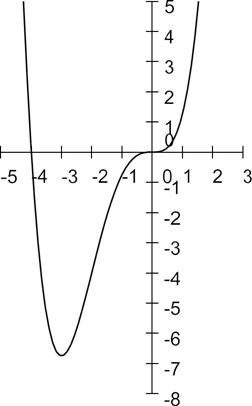
5. Найти промежутки выпуклости и точки перегиба функции: ![]() .
.
Решение
Чтобы найти промежутки выпуклости и точки перегиба, найдем вторую производную функции.
![]() .
.
![]() .
.
![]() .
.
|
x |
|
–2 |
|
1 |
|
|
|
– |
0 |
– |
0 |
+ |
|
|
вогнутая |
перегиб |
выпуклая |
перегиб |
вогнутая |
Отсюда следует, что функция
выпуклая при ![]() ,
,
вогнутая при ![]() .
.
Точки ![]() ,
, ![]() – точки перегиба.
– точки перегиба.
2. Дифференциальное исчисление функций и его приложение»
1. Провести полное исследование свойств и построить эскиз графика функции ![]() .
.
Решение.
1) Область определения функции
![]() .
.
2) Функция не является четной или нечетной, так как
![]() .
.
3) Теперь найдем точки пересечения с осями:
а) с оx: ![]() , б) с oy
, б) с oy ![]() .
.
4) Теперь найдем асимптоты.
а) 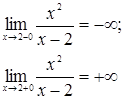
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
