Алгебра октав
откуда при u ≠ 0 следует, что у = 0. Тогда ![]() = 0 и из первого уравнения системы
= 0 и из первого уравнения системы
их = и следует, что х = 1. Итак, пара (х; у) = (1; 0) является правым единичным элементом в ![]() .
.
В случае, если и = 0, v ≠ 0, второе уравнение .системы имеет вид v13 height=23 src="images/referats/3160/image032.png">= v, откуда сразу х = 1, а из первого уравнения системы у = 0, т.е. приходим к тому же решению.
Для определения левого нейтрального элемента (единицы) относиnельно операции умножения в ![]() решим уравнение:
решим уравнение:
(х; у) ![]() (u; v) = (u; v),
(u; v) = (u; v),
в котором опять и и v одновременно не считаем равными 0, так как (0; 0) = 0U и это уравнение будет иметь любое решение. Пусть опять u ≠ 0. Тогда:
(х; у) ![]() (и; v) = (и: v)
(и; v) = (и: v) ![]() (хи -
(хи - ![]() y; vх - уū) = (и; v)
y; vх - уū) = (и; v) ![]()
![]()
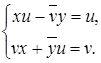
Умножим обе части первого уравнения этой системы справа на u-1=![]() , откуда:
, откуда:
x(u![]() u-1) =
u-1) = ![]() y
y![]() + u*u-1
+ u*u-1 ![]() x = 1+
x = 1+ ![]() 2
2![]() yū,
yū,
Подставим полученное значение х во второе уравнение системы:
v(1+ ![]() 2
2![]() yū) + уū= v
yū) + уū= v![]() v +
v + ![]() 2 v
2 v![]() yū + уū= v
yū + уū= v![]()
![]() yū+ уū= 0
yū+ уū= 0 ![]() (
(![]() + 1)уū =0,
+ 1)уū =0,
откуда при u ≠ 0 следует, что у = 0 и из первого уравнения системы хu = и следует, что х = 1. Итак, пара (х; у) = (1; 0) является и левым единичным элементом в ![]() . Обозначим (1; 0) = 1U,
. Обозначим (1; 0) = 1U,
11) Для определения правого симметричного для (u; v) элемента решим уравнение:
(u; v) ![]() (х: у) = (1; 0)
(х: у) = (1; 0) ![]() (их -
(их - ![]() v; уи+ v
v; уи+ v![]() ) = (1; 0)
) = (1; 0) ![]()
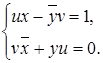
Умножим обе части первого уравнения этой системы слева на u-1=![]() 2, откуда:
2, откуда:
(u-1![]() u) x = u-1
u) x = u-1![]() v + u-1
v + u-1 ![]() x =
x =![]() 2+
2+![]() 2
2![]() v
v ![]()
![]() =
= ![]() 2 +
2 + ![]() 2
2![]() yu.
yu.
Подставим полученное значение ![]() во второе уравнение системы:
во второе уравнение системы:
v![]()
![]() +
+ 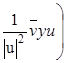 + уи= 0
+ уи= 0 ![]()
![]() 2 +
2 + ![]() 2 v
2 v![]() yu + уи= 0
yu + уи= 0 ![]() (|u|2 + |v|2) yu = - vu
(|u|2 + |v|2) yu = - vu ![]() (|u|2 + |v|2) y = - v,
(|u|2 + |v|2) y = - v,
откуда
у = - ![]() .
.
Тогда из второго уравнения системы
v![]() -
- ![]() u =0
u =0![]() v
v![]()
![]()
![]() -
- 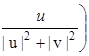 =0
=0 ![]()
![]() =
= ![]()
![]() x=
x= ![]() .
.
Итак, пара
(x; y) = 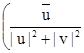 ; -
; -![]()
является правым обратным элементом для элемента (u; v) в ![]() .
.
Для определения левого симметричного элемента для элемента (u; v) относительно операции умножения в ![]() решим уравнение:
решим уравнение:
(х; у) ![]() (u; v) = (1; 0),
(u; v) = (1; 0),
в котором опять и и v одновременно не считаем равными 0. Пусть опять и ≠ 0. Тогда:
(х; у) ![]() (u; v) = (1; 0)
(u; v) = (1; 0) ![]() (xu -
(xu - ![]() y; vx + yū) = (1; 0)
y; vx + yū) = (1; 0) ![]()
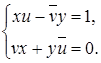
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
