Численные методы вычисления интегралов

1. Численные методы вычисления интегралов. Постановка задачи

Решая физические задачи, часто приходится вычислять значения определённых интегралов от функций . Во многих случаях, в виду того, что подлежащий вычислению интеграл не выражается через элементарные функции, прибегают к приближённым численным методам.

Преж

де всего, рассмотрим случай, когда - конечный интервал.

В таком случае, как известно, функция является ограниченной, т.е. . В этом случае наиболее часто применяемый численный метод интегрирования состоит в том, что интеграл от заменяется некоторой линейной комбинацией значений в точках :

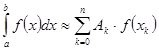(1)

Формула (1) называется квадратурной формулой, а коэффициенты - квадратурными коэффициентами или весами, абсциссы - узлами квадратурной формулы.

Методы численного интегрирования классифицируются в зависимости от того, заданы ли значения аргумента через равные промежутки или нет. Так методы Ньютона-Котеса требуют, чтобы значения были заданы с постоянным шагом, а методы Гаусса не налагают такого ограничения. Перейдём к рассмотрению этих методов.

2. Методы Ньютона-Котеса

Пусть различные точки отрезка , служащие узлами интерполяции для некоторой интерполирующей функцию функции . Тогда имеем:

(2)

где - остаточный член. Предположим, что

(3)

причём подобраны так, чтобы все интегралы

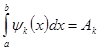(4)

можно вычислить точно. Тогда мы получаем квадратурную формулу

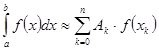(5)

2.1 Формула трапеций

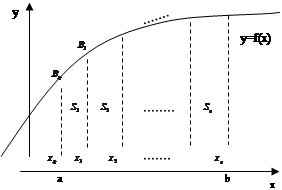Рис. 1.

а) графический вывод:

Определённый интеграл 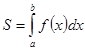, как известно, задаёт площадь криволинейной трапеции , поэтому, вписав ломаную в дугу кривой , мы получаем, что площадь криволинейной трапеции можно приближённо вычислить как сумму площадей трапеций:

(6)

Между тем, очевидно, что

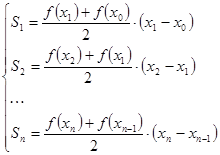(7)

Так как, в методах Ньютона-Котеса, , учитывая (6) получаем:

(8)

или, соединяя подобные члены, имеем:

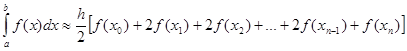(9)

Формула (9) – называется формулой трапеций.

б) Аналитический вывод:

Выведем формулу трапеции аналитическим способом. Для этого используем интерполяционный многочлен Лагранжа для отрезка , построим многочлен первой степени, который на концах отрезка принимает заданные значения . Ясно, что в таком случае интерполирующая функция имеет вид:

(10)

т.к. в методе Ньютона-Котеса , учитывая (3) и (4), из (10) получаем:

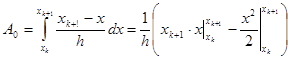
(11)

Аналогично, 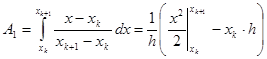, т.е.

(12)

Таким образом, получаем формулу:

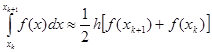(13)

тогда, используя свойство аддитивности оператора интегрирования, имеем:

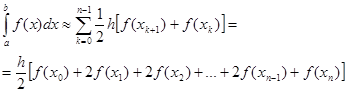(14)

где . Получили формулу (14) трапеций, которая естественно, совпадает с (9).

2.2 Формула Симпсона

Рассмотрим метод Ньютона-Котеса (т.е. ), в случае интерполяции подинтегральной функции квадратичными функциями на каждом интервале деления. В данном случае мы имеем дело с параболическим интерполированием, поэтому на каждом интервале , необходимо знание значения функции в трёх точках (т.к. имеет 3 неизвестных параметра – коэффициенты ). В качестве третьей точки на каждом отрезке - выбирается середина этого отрезка, т.е. точка .

 Скачать реферат