Алгебра октав

б) кватернионы.

Кватернионы имеют строение:

и получены некоммутативным удвоением алгебры комплексных чисел:

.

Мнимая единица удвоения j не коммутирует с единицей i, поэтому сопряжение по ней требует сопряжения также и по i и по k:

79 height=28 src="images/referats/3160/image146.png">.

Алгебраическое сопряжение в кватернионах, также как в комплексных числах, просто меняет знак у компонент при мнимых единицах:

.

То есть в кватернионах сопряжение по мнимой единице и алгебраическое сопряжение так же совпадают.

§5 .Некоторые тождества для октав

Приведем основные тождества, применимые к октавам. Тождества базируются на понятии ассоциатора, коммутатора и йорданова произведения.

()=- ассоциатор;

- коммутатор;

- йорданово произведение.

Линеаризуя тождества, несложно получить, что

& .

Таким образом, ассоциатор есть кососимметрическая функция от x, y, z. В частности:.

.

Алгебры, удовлетворяющие этому условию, называются эластичными. Таким образом, алгебра октав эластична. Покажем на основе эластичности тождество:

,

.

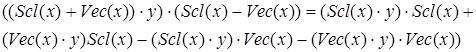В силу того, что для октав всегда есть действительное число, а в силу эластичности, получаем:

.

Таким образом, для эластичной алгебры справедливо:

.

Функция Клейнфелд:

.

Лемма1. - кососимметрическая, для любой пары равных аргументов

.

В силу правой альтернативности

.

Во всякой алгебре справедливо тождество:

.

Достаточно раскрыть все ассоциаторы. Обозначив левую часть этого равенства через , получим:

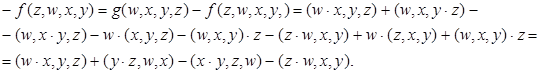
Поменяв местами: получим: .

Используя , получим, что при любых одинаковых аргументах. Из этого следуют тождества:

1) ;

2) ;

3) ;

4) .

Тождества Муфанг.

Правое тождество Муфанг: ;

Левое тождество Муфанг: ;

Центральное тождество Муфанг: .

Вопросы о строении простых алгебр в том или ином многообразии являются одними из главных вопросов теории колец. Мы уже знаем один пример простой неассоциативной альтернативной алгебры - это алгебра Кэли-Диксона. Оказывается, что других простых неассоциативных альтернативных алгебр не существует. Этот результат доказывался с нарастанием общности на протяжении нескольких десятков лет разными авторами: вначале для конечномерных алгебр (Цорн, Шафер), затем для алгебр с нетривиальным идемпотентом (Алберт), для альтернативных тел (Брак, Клейнфелд, Скорнаков), для коммутативных альтернативных алгебр (Жевлаков) и т. д. Наибольшее продвижение было получено Клейнфелдом, доказавшим, что всякая простая альтернативная неассоциативная алгебра, не являющаяся ниль-алгеброй характеристики 3, есть алгебра Кэли-Диксона. Окончательное описание простых альтернативных алгебр осуществилось после появления теоремы Ширшова о локальной нильпонентности альтернативных ниль-алгебр с тождественными соотношениями.

§6. Теорема Гурвица

6.1 Нормированные линейные алгебры

Пусть -линейная алгебра ранга п над полем действительных чисел и х, у А. Если e1, e2, ., еn - базис А, то:

х = х1е1 + х2е2 + + хпеп, у = y1е1 + y2е2 + + yпеп. .

Определение. Скалярным произведением элементов х, у А называется сумма х1у1 + х2у2 + . + хпуп.

Обозначение скалярного произведения:

(х, у) = х1у1 + х2у2 + . + хпуп.

В частности:

(х, х) = ++… +.

Скалярное произведение элементов х, уА должно удовлетворять общим условиям скалярного произведения в линейных пространствах:

1)для любых х, у А (х, у) ≥ 0 и (х, х) = 0 тогда и только тогда, когда х = 0;

2)для любых х, у А имеет место (х, у) = (у, х);

3)для любых х, у А и А R имеет место (λх, у) = (х, λу) = λ(х, у):

4)для любых х, у, z А имеет место (х, у + z) = (х, у) + (х, z).

Определение. Линейная алгебра называется нормированной, если в ней можно ввести скалярное произведение для любых х, у А таким образом, чтобы выполнялось равенство:

 Скачать реферат