Образовательный стандарт дисциплины "Системное моделирование"

Принцип проверки статистических гипотез состоит в том, что если расчетное значение попадает в область допустимых значений, то принимают гипотезу . При попадании в критическую область t=33 src="images/referats/29180/image783.png">отвергается и принимается гипотеза . Заметим, что принятие не означает, что доказана ее справедливость, а свидетельствует лишь о том, что результаты испытаний выборки не противоречат выдвинутым предположениям о свойствах объекта (генеральной совокупности). Необходимо иметь в виду, что продолжение испытаний может привести к иному заключению.

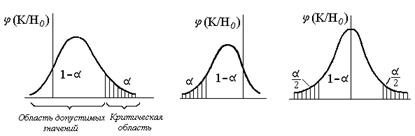
Рис. 1. Область допустимых значений и критическая область

Таким образом, правильное определение вида критической области и уровня значимости наряду с выбором статистики критерия; в основном, определяют достоверность статистического решения. В основе выбора лежит анализ последствий совершения ошибки первого или второго рода, поскольку одновременно уменьшить и невозможно. Для случая правосторонней критической области это иллюстрируется рис. 2. Если смещать вправо [не изменяя положения кривых ], то с уменьшением мощность критерия снижается. Если переместить влево, увеличивается, зато возрастает мощность критерия. Формализованные методы установления критической области основываются на том, что величины и связаны с объемом испытаний .

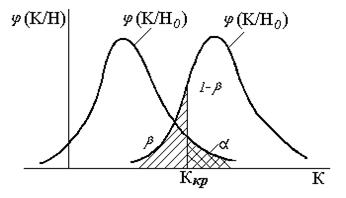
Рис. 2. Случай правосторонней критической области

Если выбрана, то при фиксированном можно руководствоваться критерием Неймана-Пирсона, в соответствии с которым из всех областей фиксированного уровня в качестве критической выбирается наиболее мощная (обеспечивающая максимум величины ). Увеличение (возрастание затрат на испытание) является единственным способом одновременного снижения и . Интуитивно значения выбираются в диапазоне . При проверке гипотез относительно технических характеристик ракет, агрегатов наземного оборудования, артиллерийских комплексов . Оценивая показатели качества (надежности, эффективности), область допустимых значений целесообразно расширить (). Более жесткие условия могут задаваться при проверке однородности характеристик контрольно-испытательной аппаратуры и свойств элементов, испытываемых в лабораторных условиях .

2. Проверка гипотез о параметрах

Рассмотрим первую группу задач статистической проверки гипотез, обеспечивающих принятие решений о средних значениях параметров. Возможны две основные задачи: проверка соответствия математических ожиданий одноименных параметров (задача проверки однородности), проверка соответствия этих математических ожиданий требованиям ТТЗ (ТУ).

В первом случае

и ,

или

, .

Во втором случае

; ; ; .

С точки зрения выбора статистики критерия, в первой задаче исходим из того, что генеральные средние неизвестны, а во второй – известны. К числу других признаков относятся: сведения о в генеральной совокупности (известно, неизвестно; или ) и объеме испытаний ( или ; или ). Заменяя в записи выборочными средними , приведем наиболее часто используемые при проверке однородности двух совокупностей статистики критериев. Если известно, то применяется статистика

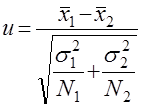. (1)

Критическое значение находится из таблицы Приложения по величине .

Гипотеза принимается, если . Формула (1) применима и в том случае, если неизвестно, но обеспечена равная точность измерений и . При малом числе испытаний и неизвестном значении используется статистика -критерия: