Образовательный стандарт дисциплины "Системное моделирование"

– конечное значение динамического ряда.

При разыгрывании данной процедуры многократно образуется совокупность случайных значений точечного прогноза. По полученной выборке значений определяются среднее значение прогноза и его дисперсия:

5 src="images/referats/29180/image232.png">; (4.1)

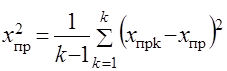, (4.2)

где – число реализаций точечного прогноза;

– разыгрываемое значение приращения на -м шаге периода упреждения в -й реализации точечного прогноза;

– значение -й реализации точечного прогноза, определяемое по зависимости (1).

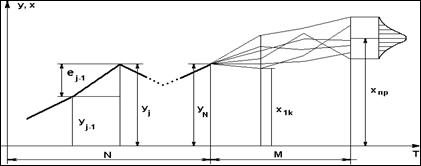
Рис. 4.1 Графическое отображение процесса случайного блуждания

Таким образом, процедура прогнозирования сводится к многократной имитации приращений на периоде упреждения и последующему определению статистических характеристик (среднего и дисперсии) реализаций точечного прогноза. График предлагаемого метода показан на рис. 4.1.

Как видно из изложенного, процедура определения характеристик прогноза при предлагаемом подходе отличается простотой, но вместе с тем характеризуется некоторой громоздкостью, обусловленной применением метода статистических испытаний. Поэтому коренным вопросом является рациональное моделирование приращений.

При наличии динамических рядов, имеющих продолжительный период основания, позволяющий получить репрезентативную выборку приращений, моделирование можно осуществлять в соответствии с определенным по этой выборке эмпирическим законом распределения приращений.

Для коротких динамических рядов можно применить допущение о нормальности отклонений значений динамического ряда от тренда. При этом допущении плотность распределения приращений также является нормальной.

При наличии на периоде основания информации малого объема (короткие динамические ряды) для моделирования приращений целесообразно использовать двумерное нормальное распределение. Двумерная плотность вероятности зависит в этом случае от пяти параметров:

,

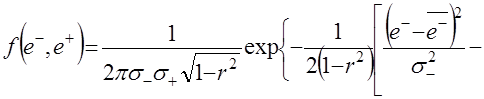
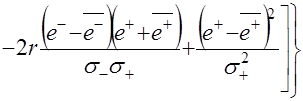где – случайные значения, математические ожидания и среднеквадратические отклонения предыдущих и последующих приращений переменной объекта прогнозирования соответственно; – коэффициент корреляции последующих приращений на предыдущие.

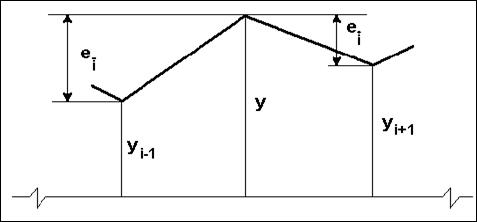
Рис. 4.2 График определения предыдущих и последующих приращений

Графически определение предыдущих и последующих приращений показано на рис. 4.2.

Очевидно, что одно и то же приращение в зависимости от того, относительно какой точки оно рассматривается, может быть как предыдущим, так и последующим. Однако первое приращение является только предыдущим.

При обработке исходного динамического ряда определяются оценки математических ожиданий и дисперсий предыдущих и последующих приращений. Множество предыдущих приращений определяется по зависимости

.

Множество последующих приращений определяется по зависимости

или

.

По множеству определяются среднее значение и оценка дисперсии предыдущих приращений:

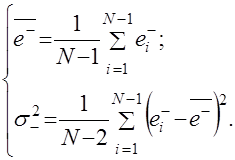(4.3)

Соответственно, по множеству определяются среднее значение и оценки дисперсии последующих приращений:

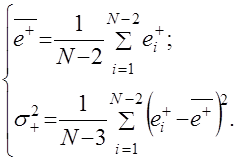(4.4)

Оценка значения коэффициента корреляции определится по зависимости

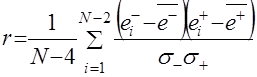. (4.5)

Для моделирования случайных приращений на периоде упреждения используется алгоритм моделирования двумерного нормального распределения. Для рассматриваемого случая моделирующая зависимость последующих приращений имеет вид

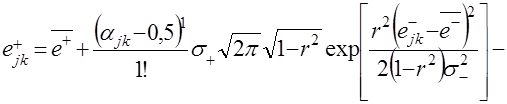
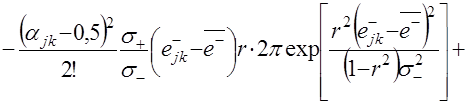
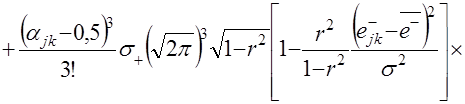
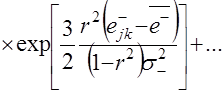(4.6)

При моделировании случайного значения на первом шаге в каждой -й реализации предыдущее значение равно значению последнего приращения на периоде основания ,то есть

При моделировании приращений на следующих шагах периода упреждения

.

Оценка коэффициента корреляции, определяемая по выборкам малых объемов, является случайной. Плотность вероятности выборочного коэффициента корреляции имеет сложный вид. При принятом допущении о нормальности распределения приращений используется нормализующее преобразование Фишера.

Случайная величина распределена нормально с параметрами

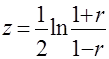; (7)

,

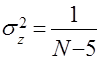где – значение выборочного коэффициента корреляции, определяемое по зависимости (4.5).