Образовательный стандарт дисциплины "Системное моделирование"

.

Вероятность называют доверительной вероятностью, а границы интервала , в которых с заданной доверительной вероятностью заключена

ошибка метода – доверительными границами.

Из теории вероятностей известно, что при нормальном законе распределения вероятность отклонения случайной величины от ее математического ожидания менее, чем на равна

, (4)

где – функция Лапласа (интеграл вероятностей);

– аргумент функции Лапласа;

– среднее квадратическое отклонение величины .

Также известно, что если производится большое число опытов, то среднее арифметическое есть также случайная величина, приближенно распределенная по нормальному закону с математическим ожиданием и средним квадратическим отклонением .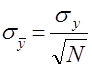

Из сказанного следует, что вероятность любого отклонения может быть вычислена по формуле [2]

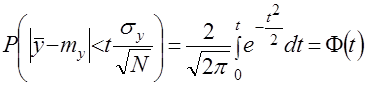. (5)

Положим

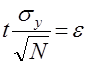, (6)

тогда получим

. (7)

Сравнивая выражения (3) и (7), найдем условие, при котором ошибка метода не превысит величину с вероятностью :

. (8)

Задаваясь доверительной вероятностью , найдем из уравнения (8) с помощью таблиц функции Лапласа численное значение . Подставив далее величину в выражение (6), получим формулу для вычисления искомого числа испытаний , при котором выполняется условие (8):

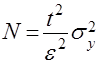. (9)

Из формулы (9) видно, что для определения необходимо еще знать величину дисперсии . Так как она неизвестна, обычно поступают следующим образом. Задаются некоторым достаточно большим значением и находят приближенное значение (статистическую оценку) дисперсии по формуле

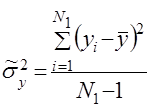. (10)

Величину подставляют в формулу (9) и находят уточненное значение . Таким образом, достигаемая точность может быть хорошо оценена только в процессе моделирования.

Задавая доверительную вероятность , получаем из формул (5), (8) доверительную оценку

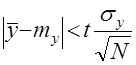(11)

с надежностью . Отсюда вытекает, что ошибка метода статистических испытаний пропорциональна величине . Следовательно, чтобы уменьшить ошибку в 10 раз (то есть, чтобы получить в ответе еще один верный знак), нужно увеличить число испытаний в 100 раз. Чтобы получить достаточно высокую точность, необходимо провести тысячи испытаний. Метод особенно эффективен при решении задач, в которых результат нужен с точностью порядка 5 – 10 %.

Мы рассмотрели точность моделирования процесса, в котором при каждом из независимых испытаний получается величина , имеющая математическое ожидание . Рассмотрим теперь случай моделирования события , вероятность появления которого в каждом из независимых испытаний равна . Обозначим через величину, равную единице, если на -м испытании произошло событие , и равную нулю, если событие не произошло. 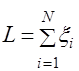Следовательно, общее число испытаний, в каждом из которых событие произошло, равно , а частота появления события равна .

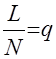Так как есть искомая величина, а – ее приближенное значение, то есть ошибка метода.

Введя снова величину , удовлетворяющую неравенство , и доверительную вероятность , получим на основании теоремы Бернулли

. (12)

Можно показать, что в этом случае необходимое число испытаний определяется по формуле