Образовательный стандарт дисциплины "Системное моделирование"

В дальнейшем проведение реальных испытаний чередовалось с мысленными опытами. При подсчете предсказанных значений натуральные значения переводились в кодированные по формуле. Как видно из табл. 2.11, переход от условий испытаний № 5 к условиям испытания № 6 не обес

печивает приращения удельной тяги. Далее в точке (рис. 3.2) была проведена контрольная серия из четырех испытаний, которая подтвердила, что дальнейшие вариации и не ведут к увеличению .

Симплексный метод заключается в том, что испытания проводятся в точках факторного пространства, соответствующих вершинам симплексов. Под -мерным симплексом подразумевают выпуклую геометрическую фигуру, имеющую вершину, соединенные прямыми отрезками-ребрами. Одномерным симплексом будет отрезок прямой, двумерным – плоский треугольник, трехмерным – тетраэдр и т.д. При планировании испытаний обычно используют правильные симплексы, у которых вершины находятся друг от друга на одинаковом расстоянии. В отличие от крутого восхождения, при использовании симплексного метода процесс изучения поверхности отклика совмещается с движением к экстремуму. Схема поиска экстремума симплекс-методом при показана на рис. 2. Сначала проводится серия испытаний в вершинах правильного -мерного симплекса (точки ) с целью выявить точку, характеризующую условия, при которых получаются худшие результаты. Следующую серию испытаний проводят в вершинах нового симплекса, который получают заменой точки, соответствующей худшему результату (точка ), ее зеркальным отображением. Тем самым достигается смещение центра тяжести симплекса в направлении экстремума. В дальнейшем процедура повторяется, и образуется последовательность симплексов, перемещающихся в факторном пространстве в направлении к экстремуму. На близость экстремума указывает начинающееся вращение симплекса вокруг одной из его вершин.

Шаговое движение к экстремуму продолжается до тех пор, пока будет достигнута «почти стационарная область», которая не может быть описана линейной моделью, и где значимы совместные (квадратичные) эффекты воздействия.

Близость «почти стационарной области» можно установить, если провести серию испытаний в центре плана и определить значение выходного параметра . Вычисляемое для линейной модели значение при реализации ПФП или ДФП в «почти стационарной области» является совместной оценкой для свободного члена и суммы квадратов членов. Следовательно, разность дает представление о кривизне поверхности отклика.

«Почти стационарную область» в большинстве случаев с приемлемой точностью можно описать уравнением второго порядка

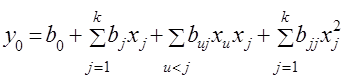. (18)

Поскольку для отыскания раздельных оценок параметров число уровней должно быть на единицу больше степени полинома, число уровней должно быть не менее трех. Однако применение ПФП типа приведет к резкому возрастанию количества испытаний. Для сокращения можно использовать центральные композиционные планы (ЦКП). Ядро ЦКП составляют ПФП или ДФП: ПФП, если число факторов , и ДФП при . Это приводит к тому, что если после реализации ПФП (ДФП) гипотеза о линейности модели не подтвердилась, нет необходимости проводить испытания заново. Для получения модели второго порядка достаточно добавить к ПФП (ДФП) несколько специальным образом подобранных точек, в которых и провести дополнительную серию испытаний.

Пусть для получения линейной модели реализован ПФП . Согласно рис. 1,б экспериментальные точки лежат в вершинах куба. Если линейная модель неадекватна, то в план включается так называемых «звездных точек» с координатами , расположенных на сфере диаметром (рис. 3). Таким образом, каждая из точек плана лежит на координатных осях на расстоянии от центра плана, называемым звездным плечом . Центром плана является центральная точка прямоугольника, если число факторов , куба при , гиперкуба, когда . Наличие звездных точек, собственно, и задает центральный композиционный план.

Представление о положении звездных точек в факторном пространстве дают следующие примеры: при и ядре плана, образованном ПФП , величина звездного плеча ; если , а в ядре реализован ПФП , то ; при и ПФП . Общее число испытаний при реализации ЦКП

,

где – ядро плана, – число звездных точек; – количество испытаний, проводимых в центре плана.

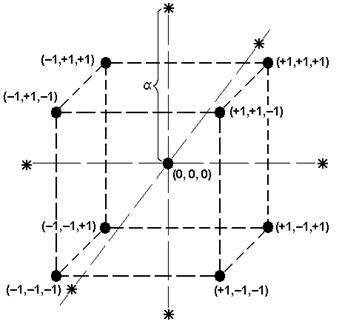
Рис. 3. «Звездные точки» с координатами