Образовательный стандарт дисциплины "Системное моделирование"
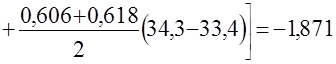 .
.
Значение интеграла 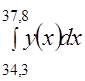 будет
будет
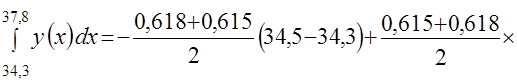
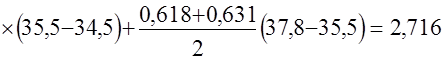 .
.
Полученные коэффициенты подставляются в систему уравнений (4.26):
ght=67 src="images/referats/29180/image369.png">
Решая эту систему, определяются
![]() .
.
Затем находится значение первой производной в начальной точке путем подстановки в уравнение (4.23) вычисленных коэффициентов и ![]() .
.
Тогда
![]() .
.
Для ![]() базисное уравнение имеет вид
базисное уравнение имеет вид
![]() или
или ![]() .
.
Таким образом, получены все параметры. Подставив в уравнение функции с гибкой структурой значение первой производной и значение ![]() , можно получить
, можно получить
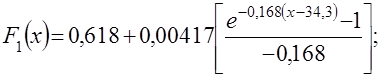
![]() .
.
Подстановкой вместо ![]() его перспективного значения на определенный год определяется ожидаемая величина коэффициента выпуска. Необходимо отметить, что основной задачей при использовании ФГС для прогноза является определение корней базисного уравнения
его перспективного значения на определенный год определяется ожидаемая величина коэффициента выпуска. Необходимо отметить, что основной задачей при использовании ФГС для прогноза является определение корней базисного уравнения ![]() , значения которых зависят от коэффициентов
, значения которых зависят от коэффициентов ![]() . Последние должны определяться из принципа оптимальной аппроксимации, заключающегося в минимизации остатка
. Последние должны определяться из принципа оптимальной аппроксимации, заключающегося в минимизации остатка ![]() и установлении таких значений коэффициентов
и установлении таких значений коэффициентов ![]() , для которых значение остатка в каждой точке таблицы исходных данных не превышает некоторой заданной величины (ошибки аппроксимации). При машинной реализации метода, базирующегося на применении ФГС, необходимо принимать допущение о дифференцируемости функции
, для которых значение остатка в каждой точке таблицы исходных данных не превышает некоторой заданной величины (ошибки аппроксимации). При машинной реализации метода, базирующегося на применении ФГС, необходимо принимать допущение о дифференцируемости функции ![]()
![]() раз, с учетом которого можно записать, что
раз, с учетом которого можно записать, что
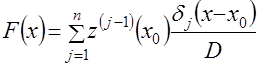 ; (4.27)
; (4.27)
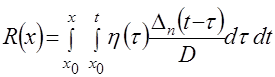 , (4.28)
, (4.28)
где ![]() – значение производной функции
– значение производной функции ![]()
![]() порядка в точке
порядка в точке ![]() ;
;
![]() – выражение, получаемое из определителя
– выражение, получаемое из определителя
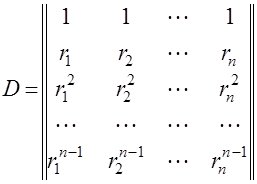 (4.29)
(4.29)
заменой последней строки определителя на функции вида ![]() ,
, ![]() ;
;
![]() . (4.30)
. (4.30)
Значения коэффициентов ![]() определяются в результате решения уравнения (4.30) путем приравнивания его к нулю. В связи с тем, что производные
определяются в результате решения уравнения (4.30) путем приравнивания его к нулю. В связи с тем, что производные ![]() неизвестны, переходят к системе линейных алгебраических уравнений [1], [2] вида
неизвестны, переходят к системе линейных алгебраических уравнений [1], [2] вида
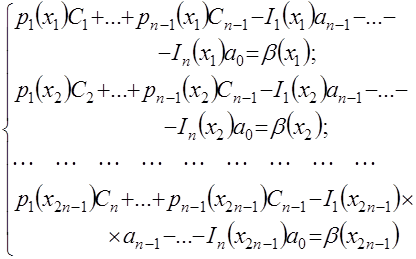 , (4.31)
, (4.31)
где 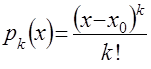 ,
, ![]() ;
;
![]() – постоянная интегрирования;
– постоянная интегрирования; ![]() ;
;
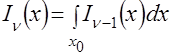 ,
, ![]() ,
, ![]() ;
;
![]() ;
; ![]() .
.
Результатом решения этой системы является определение коэффициентов ![]() , что позволяет по базисному уравнению вычислить параметры
, что позволяет по базисному уравнению вычислить параметры ![]() . Неизвестные
. Неизвестные ![]() как следует из (4.18), (4.27), равны значениям производных функций в точке
как следует из (4.18), (4.27), равны значениям производных функций в точке ![]() , то есть
, то есть
![]() .
.
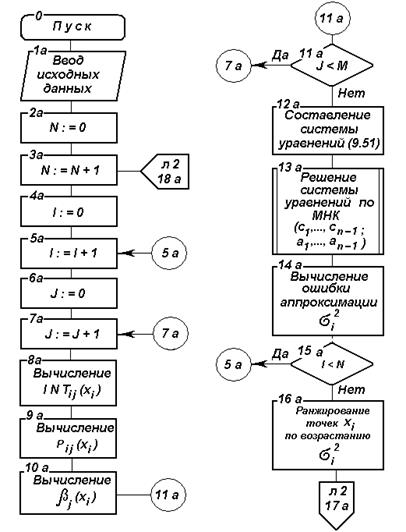
Рис. 4.6 Блок-схема алгоритма параметрического прогнозирования на основе ФГС
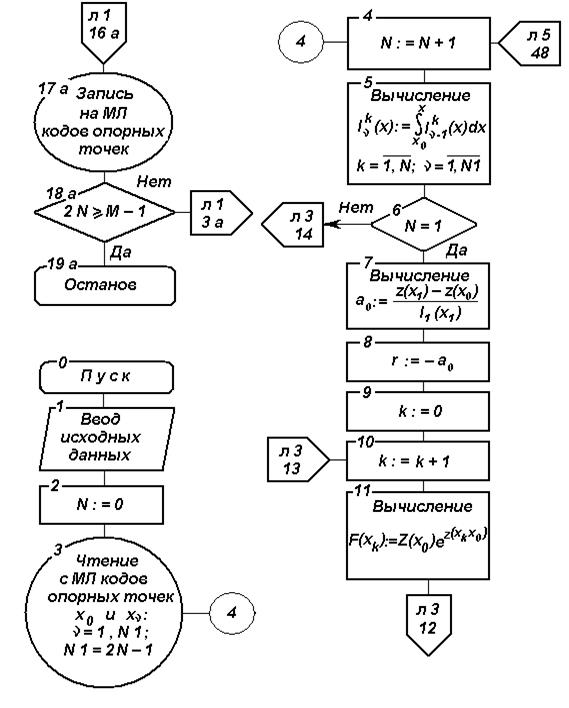
Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС (продолжение)
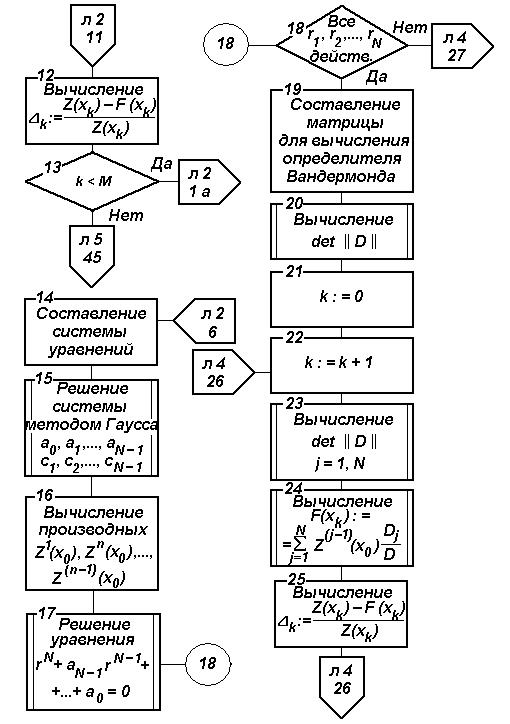
Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС (продолжение)
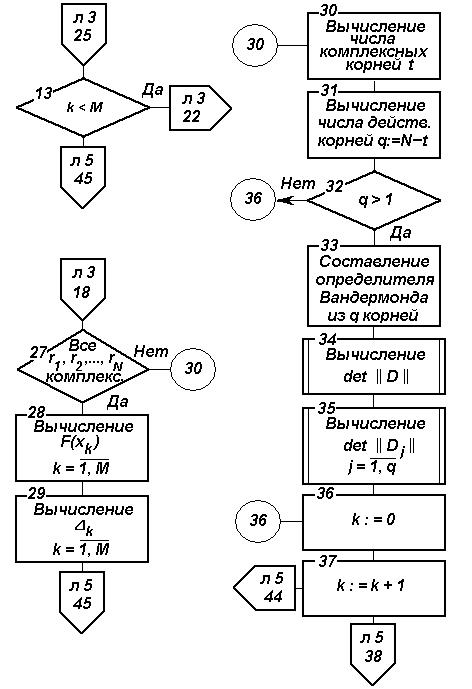
Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС (продолжение)
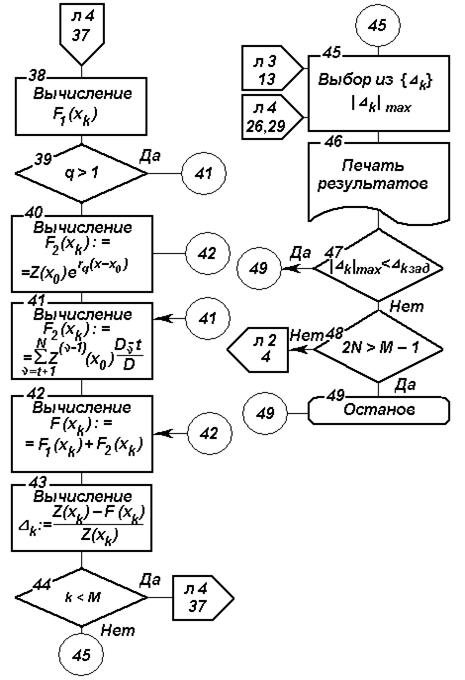
Рис. 4.6. Блок-схема алгоритма параметрического прогнозирования на основе ФГС (продолжение)
На основе изложенного разработан алгоритм параметрического прогнозирования, блок-схема которого изображена на рис. 4.6.
Согласно работам [1], [2] можно утверждать, что ошибка аппроксимации в значительной степени зависит от системы опорных точек ![]() и
и ![]() , которые необходимо выбрать для вычисления коэффициентов при неизвестных
, которые необходимо выбрать для вычисления коэффициентов при неизвестных ![]() и
и ![]() и свободных членов системы уравнений (31). Поэтому в рамках алгоритма имеется специальная процедура выбора системы опорных точек (блоки 1–19), использование которой обеспечивает минимальную ошибку аппроксимации. Смысл этой процедуры сводится к следующему:
и свободных членов системы уравнений (31). Поэтому в рамках алгоритма имеется специальная процедура выбора системы опорных точек (блоки 1–19), использование которой обеспечивает минимальную ошибку аппроксимации. Смысл этой процедуры сводится к следующему:
в качестве начальной точки ![]() последовательно выбирается каждая точка
последовательно выбирается каждая точка ![]() таблицы исходных данных (блоки 4а, 5а, 15а);
таблицы исходных данных (блоки 4а, 5а, 15а);
Другие рефераты на тему «Педагогика»:
- Особенности становления самооценки у детей старшего дошкольного возраста с нарушением слуха
- Технология раннего и интенсивного обучения грамоте по методу Н.А. Зайцева
- Физическое воспитание во взаимосвязи с нравственным воспитанием в младшем школьном возрасте
- Новые технологии воспитательного процесса
- Саморегуляция одаренного ребенка как условие социальной адаптации
Поиск рефератов
Последние рефераты раздела
- Тенденции развития системы высшего образования в Украине и за рубежом: основные направления
- Влияние здоровьесберегающего подхода в организации воспитательной работы на формирование валеологической грамотности младших школьников
- Характеристика компетенций бакалавров – психологов образования
- Коррекционная программа по снижению тревожности у детей младшего школьного возраста методом глинотерапии
- Формирование лексики у дошкольников с общим недоразвитием речи
- Роль наглядности в преподавании изобразительного искусства
- Активные методы теоретического обучения
