Образовательный стандарт дисциплины "Системное моделирование"

Первый столбец используется только для выполнения расчетов ( – фиктивная переменная). В последнем столбце записываются результаты испытания.

Порядок перехода от плана к плану 37 src="images/referats/29180/image499.png">показан в табл. 2. Аналогично методом «перевала» можно перейти к планам с большим числом факторов.

Таблица 2

Приведенные в табл. 1 и 2 матрицы планирования обладают свойствами ортогональности, симметричности и нормировки.

Свойство симметричности относительно центра опыта заключается в том, что алгебраическая сумма элементов вектор-столбцов каждого из факторов равна нулю:

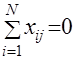; ; . (4)

Условие нормировки подтверждается равенством суммы квадратов элементов каждого столбца числу опытов:

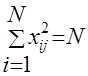; . (5)

Свойство ортогональности определяется равенством нулю произведений любых двух вектор-столбцов:

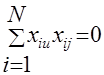;. (6)

Предполагается, что при перемножении элементов с одноименными знаками получаем , с разноименными .

Свойство ортогональности позволяет резко уменьшить трудоемкость вычислений коэффициентов регрессии, так как матрица нормальных уравнений становится диагональной, причем ее диагональные элементы равны числу испытаний , заданных матрицей ПФП.

Воспользуемся матрицей планирования (табл.1) для получения уравнения регрессии вида

. (7)

При вычислении оценок коэффициентов регрессии по формуле последовательно получим

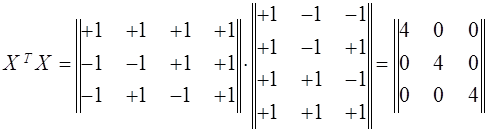
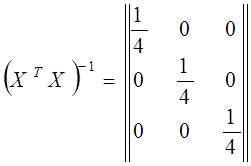
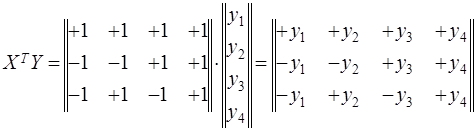
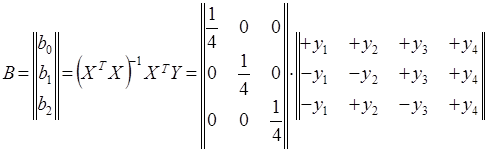
Отсюда

; ;

; .

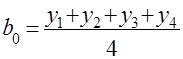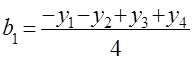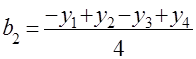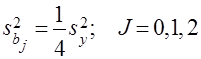Таким образом, каждый из коэффициентов вычисляется независимо и по простой формуле, которая в общем случае имеет вид

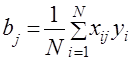. (8)