Образовательный стандарт дисциплины "Системное моделирование"

при зафиксированном значении вычисляются значения (блоки 6а–11а);

составляется система уравнений (4.31) (блок 12а);

решается система уравнений (4.31) по МНК и определяются значения Си , idth=120 height=29 src="images/referats/29180/image408.png">(блок 13а);

устанавливается структура модели, например в виде регрессионного уравнения

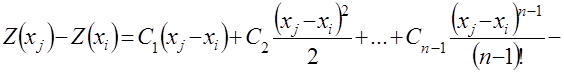
(4.32)

параметры которого определены выше, и задают ошибку аппроксимации по зависимости (блок 14а)

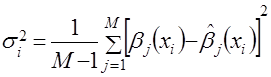, (4.33)

где – число наблюдений над прогнозируемой характеристикой;

осуществляются ранжировка исходных данных по возрастанию , выбор опорных точек по правилу (блок 16а)

и их запись;

описанная процедура повторяется для каждого значения (блоки 2а, За, 18а).

После выбора опорных точек в алгоритме предусмотрены операторы по подготовке к составлению системы уравнений порядка. С этой целью по соответствующим зависимостям методом численного интегрирования (методом трапеций) вычисляются , а также значения и (блок 5). При этом

.

Если число членов ФГС-модели , то значения параметров функции и относительного отклонения функции от в -й точке рассчитываются в соответствии с выражениями блоков 7–3. На основе выбора из множества значения и сравнения его с заданным (блоки 45, 47), принимается решение либо продолжать усложнять модель, либо удовлетвориться достигнутой сложностью. При осуществляется составление системы уравнений порядка вида (4.31) (блок 14) и решение ее методом Гаусса относительно параметров и постоянных интегрирования (блок 15).

В блоке 16 осуществляется вычисление параметров

по зависимостям

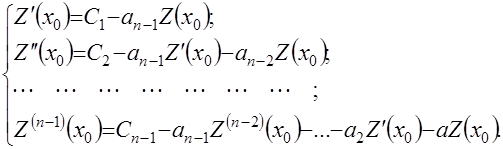(4.34)

Вычисление корней базисного уравнения производится методом Ньютона с использованием стандартной программы (блок 17). Поскольку в общем случае корни уравнения могут быть действительными, комплексными или действительными и комплексными, в блоках 18, 27 производится их анализ с целью определения дальнейшей расчетной схемы. При условии, что все корни действительные, функция принимает вид

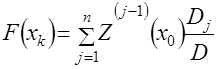, (4.35)

где – степенной определитель -го порядка (4.29), значение которого вычисляется методом перекрестного умножения (блоки 19, 20);

– определитель, получаемый из (4.29) заменой -й строки на функции – блок 23;

– вычисленная ранее производная.

Значение функции в каждой точке и ее отклонения вычисляются в блоках 21, 22, 24-26. При подстановке значений , и зависимость (4.35) принимает вид суперпозиции экспоненциальных законов, параметрами которых являются аргументы прогнозирующих зависимостей.

Если все корни комплексные, то имеет вид

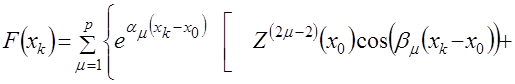
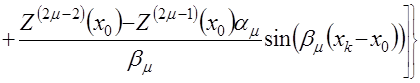,(4.36)

где – нечетное натуральное число;

– действительная часть корня; ; .

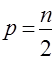Значения функции и ее отклонения вычисляются в блоках 28, 29. Если в результате анализа устанавливается, что корней комплексные, а корней действительные, то принимает вид

,

где вычисляется по зависимости (4.36) с использованием корней блок 38); при вычисляется по зависимости (4.35) с использованием корней (блоки 33, 34, 35, 41), при – в соответствии с блоками 32, 39, 40. Значения функции и ее отклонения от вычисляются в блоках 36, 37, 42, 43, 44. Результаты расчетов выводятся на печать. После вычисления функции и в каждом из приведенных случаев выбирается максимальное значение отклонения , которое сравнивается с заданным (блоки 45, 47).