Образовательный стандарт дисциплины "Системное моделирование"
![]() – постоянные действительные параметры;
– постоянные действительные параметры;
![]() – специальный (степенной) определитель
– специальный (степенной) определитель ![]() -го порядка;
-го порядка;
![]() – функция, получаемая из определителя
– функция, получаемая из определителя
заменой строки ![]() на соответствующие функции
на соответствующие функции
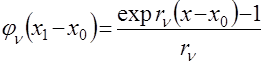 ,
, ![]() .
.
При ![]() функция с гибкой структурой имеет вид
функция с гибкой структурой имеет вид
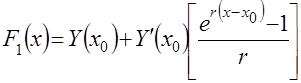 , (4.19)
, (4.19)
где ![]() – начальное значение функции
– начальное значение функции ![]() и ее производной в точке
и ее производной в точке ![]() ;
; ![]() – корень специального уравнения
– корень специального уравнения ![]() , в рассматриваемом случае
, в рассматриваемом случае ![]() .
.
Нахождение параметров функции ![]() связано с минимизацией базисной функции
связано с минимизацией базисной функции
![]() . (4.20)
. (4.20)
Далее представляется логичным определить порядок расчета параметров ФГС. В том случае, когда имеется всего один фактор, базисная функция имеет вид
![]() . (4.21)
. (4.21)
При ![]() на рассматриваемом отрезке функция
на рассматриваемом отрезке функция ![]() равна нулю, и если проинтегрировать выражение (2.4.21) для того, чтобы избавиться от производных, можно получить
равна нулю, и если проинтегрировать выражение (2.4.21) для того, чтобы избавиться от производных, можно получить
![]() . (4.22)
. (4.22)
Подставляя в это уравнение значение начальной точки, легко установить, что величина первой производной связана со значением величины ![]() и
и ![]() соотношением
соотношением ![]() . (4.23)
. (4.23)
Если проинтегрировать уравнение (22) еще раз, то можно записать выражение вида
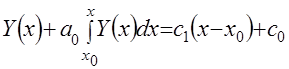 . (4.24)
. (4.24)
При условии, что ![]() , определяется
, определяется ![]() . Тогда уравнение (4.24) целесообразно представить следующей зависимостью:
. Тогда уравнение (4.24) целесообразно представить следующей зависимостью:
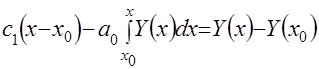 . (4.25)
. (4.25)
Из этого уравнения видно, что оно содержит неизвестные величины. Теперь значение интеграла можно вычислить, так как функция ![]() УМ задана таблицей, а для определения
УМ задана таблицей, а для определения ![]() и
и ![]() можно образовать систему двух уравнений с двумя неизвестными на основе уравнения (4.25). Это нетрудно сделать, если подставить в (4.25) значение еще двух точек, взятых из временного ряда. Тогда
можно образовать систему двух уравнений с двумя неизвестными на основе уравнения (4.25). Это нетрудно сделать, если подставить в (4.25) значение еще двух точек, взятых из временного ряда. Тогда
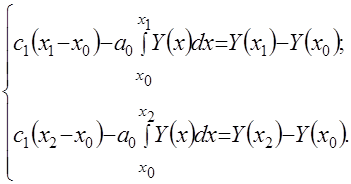 (4.26)
(4.26)
После вычисления данных интегралов находятся неизвестные коэффициенты ![]() и
и ![]() . Затем определяется значение первой производной путем подстановки в уравнение (4.23)
. Затем определяется значение первой производной путем подстановки в уравнение (4.23) ![]() ,
, ![]() и
и ![]() . Корень базисного уравнения равен параметру
. Корень базисного уравнения равен параметру ![]() со знаком минус. Вычисленные параметры подставляются в формулу ФГС (4.19) для получения математического выражения формы связи между
со знаком минус. Вычисленные параметры подставляются в формулу ФГС (4.19) для получения математического выражения формы связи между ![]() и
и ![]() .
.
В качестве примера применения функции с гибкой структурой для прогнозирования в военном деле рассматривается задача по определению вида зависимости между коэффициентом выпуска серийных образцов условных технических систем и объемом задач, выполняемых с помощью данных образцов. Эта зависимость в дальнейшем используется для получения прогноза. Исходные данные представлены в табл. 1.
Таблица 1
|
|
0,597 |
0,597 |
0,608 |
0,618 |
0,615 |
0,618 |
0,631 |
|
|
31,2 |
32,3 |
33,4 |
34,3 |
34,5 |
35,5 |
37,8 |
Из этой таблицы выбираются значения трех опорных точек, одна из которых (начальное значение) должна лежать в середине ряда с тем, чтобы полученная функция одинаково точно приближала данное значение как в конце, так и в начале ряда. Следовательно,
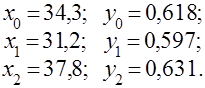
Определяются коэффициенты уравнения (4.26):
![]()
Следующий шаг – переход к вычислению необходимых интегралов (рис. 4.5).
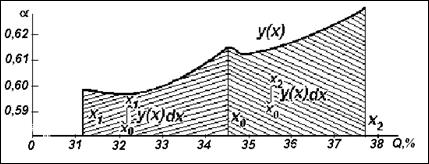
Рис. 4.5 Определение необходимых интегралов для ФГС
Интеграл вида 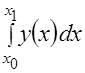 есть площадь, ограниченная графиком и значениями
есть площадь, ограниченная графиком и значениями ![]() , равными 34,3 и 31,2. Так как верхний предел интеграла меньше нижнего, то значение интеграла отрицательное. Площадь, ограниченная значениями
, равными 34,3 и 31,2. Так как верхний предел интеграла меньше нижнего, то значение интеграла отрицательное. Площадь, ограниченная значениями ![]() равными 34,3 и 31,2, будет складываться из площадей трех трапеций:
равными 34,3 и 31,2, будет складываться из площадей трех трапеций:
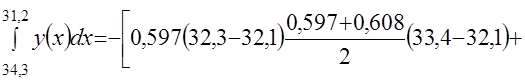
Другие рефераты на тему «Педагогика»:
- Развитие алгоритмического мышления у младших школьников на уроках математики
- Профилактика безнадзорности и правонарушений несовершеннолетних
- Обучение чтению как средство развития личности и формирования её базовой культуры
- Преодоление нарушений свистящих звуков у дошкольников с фонетико-фонематическим недоразвитием с учетом этапа коррекционной работы
- Развитие технического мышления учащихся в процессе трудового обучения
Поиск рефератов
Последние рефераты раздела
- Тенденции развития системы высшего образования в Украине и за рубежом: основные направления
- Влияние здоровьесберегающего подхода в организации воспитательной работы на формирование валеологической грамотности младших школьников
- Характеристика компетенций бакалавров – психологов образования
- Коррекционная программа по снижению тревожности у детей младшего школьного возраста методом глинотерапии
- Формирование лексики у дошкольников с общим недоразвитием речи
- Роль наглядности в преподавании изобразительного искусства
- Активные методы теоретического обучения
