Нормированные пространства

Доказательство.

Возьмем из . По определению существует последовательность из такая, что стремится к , при стремящемся к .

Докажем, что из будет фундаментальной последовательностью. Тогда, т.к. полное, последовательность будет сходящейся.

Возьмем произвольное положительное число . Найдем номер , для которого выполняется .Тогда

. Следовательно, последовательность фундаментальная.

Пусть стремится к . Определим оператор равенством .

а) Проверим корректность определения оператора .

Итак, стремится к , стремится к . Возьмем другую последовательность , имеющую в пределе . Тогда будет стремится к некоторому элементу .Составим новую последовательность Ее пределом будет . Пусть соответствующая последовательность стремится к . Из последней можно выбрать две подпоследовательности и , сходящиеся соответственно к и .Следовательно, и , т.е. и совпадают.

б) Докажем линейность оператора А. Пусть Х; - произвольные числа. Рассмотрим элемент . По определению существуют последовательности {xn},{yn}, такие, что . Тогда .

.

Получили , что и означает по определению линейность оператора А. При этом, т.к. если , то в качестве можно взять для всех n. Тогда и .

в) Докажем непрерывность оператора А.

Возьмем . , .

. По теореме о предельном переходе в неравенстве будет выполняться неравенство . Т.к. по определению - это наименьшая из констант, удовлетворяющих данному неравенству, то . (*)

С другой стороны, по определению , . Так как , то . (**)

Учитывая неравенства (*) и (**) , установили равенство . Таким образом, утверждение доказано.

Определение. Функция называется простой, если она представляет собой конечную линейную комбинацию характеристических функций попарно непересекающихся измеримых множеств , где .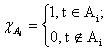

Теорема Лебега. Если последовательность на сходится к и при всех , где суммируема на, то предельная функция суммируема на и .

 Скачать реферат