Нормированные пространства
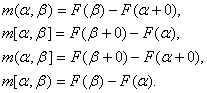
Таким образом, функция ![]() , которая каждому сегменту ставит в соответствие меру этого сегмента, будет:
, которая каждому сегменту ставит в соответствие меру этого сегмента, будет:
1. принимать действительные неотрицательные значения;
2. аддитивной, т.е. мера объединения есть сумма мер этих сегментов.
Применив стандартное распрост
ранение меры, получим меру на некоторой ![]() - алгебре.
- алгебре.
Определение. Меру ![]() , получающуюся с помощью такого построения, называют мерой Лебега – Стилтьеса, отвечающей функции
, получающуюся с помощью такого построения, называют мерой Лебега – Стилтьеса, отвечающей функции ![]() , а саму функцию
, а саму функцию ![]() называют производящей функцией этой меры.
называют производящей функцией этой меры.
Определение. Пусть ![]() - мера на R, порожденная монотонной функции
- мера на R, порожденная монотонной функции ![]() . Для этой меры обычным образом определяется класс суммируемых функций и вводится понятие интеграла Лебега
. Для этой меры обычным образом определяется класс суммируемых функций и вводится понятие интеграла Лебега ![]() .
.
Такой интеграл, взятый по мере ![]() , отвечающей производящей функции
, отвечающей производящей функции ![]() , называется интегралом Лебега – Стилтьеса и обозначается
, называется интегралом Лебега – Стилтьеса и обозначается ![]() .
.
Теперь докажем факт, который используется при доказательстве интерполяционной теоремы.
Предложение 2. ![]()
![]()
![]()
![]() и для
и для ![]()
![]() и
и ![]() , тогда
, тогда
(1) 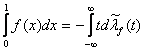 , и если
, и если ![]() , и
, и ![]() , то
, то
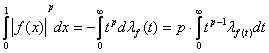 . (2)
. (2)
Доказательство.
Равенство (1) следует из определения интегралов Лебега и Лебега – Стилтьеса:
Если ![]() - последовательность разбиений действительной оси:
- последовательность разбиений действительной оси:
![]() , и
, и ![]() , то интегралы
, то интегралы 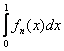 , где
, где ![]() , если
, если ![]() , стремятся при
, стремятся при 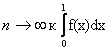 .
.
С другой стороны:
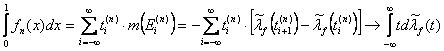 при
при ![]() .
.
Это и доказывает равенство (1).
Пусть теперь ![]() . По (1), учитывая, что
. По (1), учитывая, что ![]()
![]() , получаем
, получаем 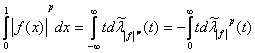 (2’)
(2’)
При 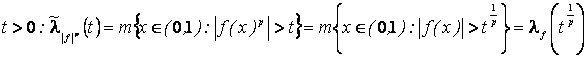
Следовательно, из соотношения (2’), делая замену переменных ![]() , получим первое равенство (2).
, получим первое равенство (2).
Далее, для любого ![]() выполняется
выполняется
![]()
(интегрирование по частям: ![]() ).
).
Для доказательства второго равенства в (2) достаточно устремить в последнем соотношении число ![]() к
к ![]() и использовать оценку:
и использовать оценку:
![]() при
при![]() .
.
Предложение 2 доказано.
Замечание. Если функция ![]() задана на
задана на ![]() , то, применяя равенство (2) для функции
, то, применяя равенство (2) для функции ![]() ,
, ![]() , и учитывая, что
, и учитывая, что ![]() , получим
, получим
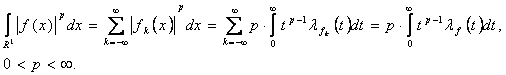 (3)
(3)
Глава II. Интерполяция в пространствах суммируемых функций.
§1. Теорема Марцинкевича и ее применение.
Одной из важнейших в теории интерполяции является теорема Ж.Марцинкевича, доказанная им в 1939 году. Прежде чем рассмотреть теорему, докажем предложение.
Пусть дана функция ![]() . Положим для
. Положим для ![]()
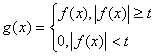 ,
, 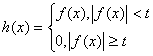 .
.
Предложение 3. Пусть ![]() ,
, ![]() , для любого положительного числа
, для любого положительного числа ![]()
![]() и
и ![]() – функции, описанные выше. Тогда
– функции, описанные выше. Тогда ![]() .
.
Доказательство.

 |  |  |
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
