Нормированные пространства

2) Проверим, что оператор Т типа , т.е. .

Рассмотрим случай, когда функция g имеет вид: .

.

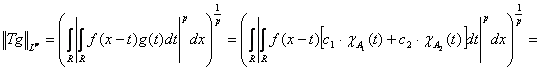
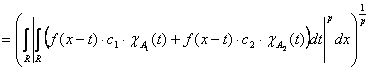Обозначим .

Тогда правая часть равенства примет вид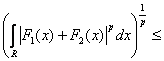

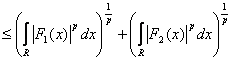
по неравенству Минковского. (1)

Рассмотрим первое слагаемое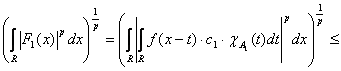

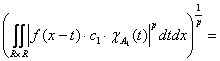
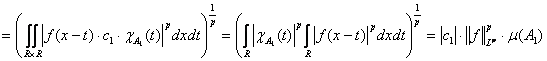(2) Аналогично второе слагаемое

. (3)

Таким образом, учитывая (1),(2),(3), получим . Найдем

, т.к. .

Далее имеем

. В результате, ,т.к. , то и равна некоторому числу.

Совершенно аналогично доказывается для случая, когда .

1) Таким образом, из пунктов I.1 и I.2 получим, что типа и , и,

следовательно, будет типа при условии 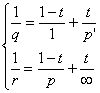, где .

; , т.е. , что и дано по условию.

Таким образом, применив теорему Рисса – Торина, установили истинность доказываемого утверждения для всех простых функций .

II. Пусть – произвольная функция из .

По предложению 4 множество простых функций всюду плотно в .

По утверждению 4 оператор свертки можно распространить на и тогда доказываемый факт верен для любой функции из . Теорема доказана.

Глава III. Пространства суммируемых последовательностей.

§1. Основные понятия.

Рассмотрим применение теории интерполяции для пространств .

Пусть {mz}zÎZ - последовательность неотрицательных чисел. Определим на множестве Z меру следующим образом: для любого целого числа . Пространство суммируемых со степенью p последовательностей относительно меры m, то есть таких, что обозначается .

Так как мера m определена на множестве всех подмножеств множества Z, то любую последовательность можно рассматривать как измеримую функцию. Обозначим через линейное пространство всех последовательностей.

Определение. Число называется нормой последовательности xn из lp(m,Z).

В случае, если для всех z, то получим классическое пространство lp(Z) последовательностей, суммируемых со степенью p .

Определение. Оператор Т, действующий из пространства в называется оператором слабого типа (p,p), если , где , и оператором типа (p,p), если .

В этом случае остается справедливым следующий факт: любой оператор типа есть оператор слабого типа . Прежде чем установить его истинность, докажем утверждение, которое для этого понадобится.

Утверждение 5. Пусть дана последовательность из с неотрицательными членами. Тогда .

 Скачать реферат