Нормированные пространства

Доказательство.

Считаем, что . Фиксируем функцию и положительное число . Оценим величину

Пусть и функции, описанные выше.

Тогда и по замечанию 2.

Следовательно, .

Используя оценки слабого типа , находим, что при положительном

.

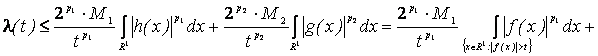
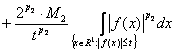Из последнего неравенства и формулы (3) из замечания 1 получаем

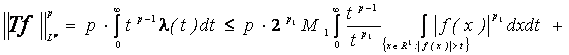
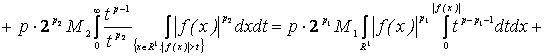
, т.е. оператор Т имеет тип . Теорема доказана.

В качестве применения этой теоремы рассмотрим следующий пример.

Утверждение 2. Пусть . Тогда оператор будет непрерывным оператором в пространстве , .

Доказательство.

Рассмотрим два случая, когда и . Докажем, что оператор является оператором типа для этих случаев. Тогда по предложению 1 будет оператором слабого типа для и . Применив интерполяционную теорему Марцинкевича, получим, что – оператор типа для любого , а это равносильно его непрерывности.

1) и . Докажем, что найдется число , такое, что

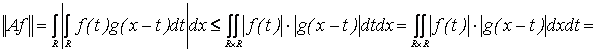
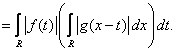
Учитывая последнее равенство и то, что для любого действительного числа верно , получим

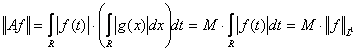, где .

2).

Нужно доказать, что

Для почти всюду выполняется неравенство: . (*)

Обозначим , .

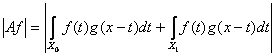. Так как , то .

Исходя из последнего соотношения и неравенства (*), получаем

.

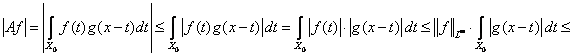
Таким образом, доказали, что оператор свертки непрерывен в пространстве для любого р³1.

§2. Интерполяционная теорема Рисса – Торина

и ее применение.

Прежде чем рассмотреть теорему Рисса – Торина и ее приложение, приведем определения и докажем факты, связанные с теорией банаховых пространств, которые понадобятся для этого.

Определение. Последовательность метрического пространства Х называется фундаментальной, если .

Верно следующее утверждение.

Утверждение. Если последовательность сходится, то она фундаментальная.

Обратно верно не всегда.

Определение. Метрическое пространство называется полным, если в нем любая фундаментальная последовательность сходится.

Определение. Если пространство , порожденное нормой, является полным, то линейное нормированное пространство называется банаховым.

Определение. Пусть – банахово пространство, – подпространство в . называется всюду плотным в Х, если , т.е. , такая, что .

Утверждение 4 . Пусть оператор , где плотно в– банахово пространство. Тогда оператор можно распространить на , т.е. существует оператор , такой, что и .

 Скачать реферат