Нормированные пространства

Доказательство.

Обозначим . Нужно доказать, что .

. Получили, что .

Утверждение доказано.

Предложение 5. Люб

ой оператор типа есть оператор слабого типа .

Доказательство.

Дано, что и . Доказать, что

.

Возьмем произвольное положительное число . По утверждению 5

. По условию . Тогда , что и требовалось доказать.

Легко увидеть, что теорема Марцинкевича будет справедлива и для операторов, действующих из пространств в пространство .

§2. Связь между коэффициентами Фурье - периодической функции и ее нормой в .

Теория интерполяции имеет многочисленные приложения в теории рядов Фурье.

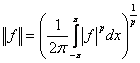Определение. Пусть -периодическая функция, такая что . Нормой в пространстве называется число , а коэффициентами Фурье функции называются числа .

Для функций из пространства выполняется равенство .

В случае других значений это, вообще говоря, не верно. Однако можно указать следующую оценку.

Предложение 6. Пусть периодическая функция из . Тогда для любого числа из отрезка [1,2] существует константа , такая, что .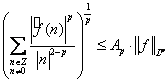

Доказательство.

Рассмотрим оператор и определим меру , т.е. оператор действует из в .

1) Докажем, что оператор слабого типа : .

Зафиксируем произвольное положительное число .

.

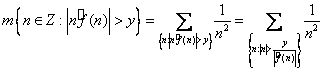Пусть 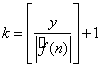. Тогда . (2)

Далее имеем

.

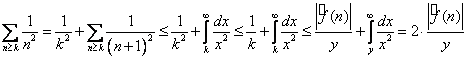Учитывая равенства (1) и (2), получим, что .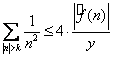

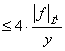В результате нашли константу , такую, что .

2) Докажем, что типа : .

Уже говорилось, что для функций из пространства выполняется равенство 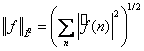. (3)

. По неравенству (3) 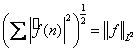. По предложению 5 оператор будет слабого типа .

3) По теореме Марцинкевича будет типа для любого из интервала (1,2), т.е. , что и требовалось доказать.

Литература.

1. Вулих Б.З. Краткий курс теории функций вещественной переменной. «Наука», Москва, 1965.

2. Кашин Б.С., Саакян А.А. Ортогональные ряды. «Наука», Москва, 1984.

3. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. «Наука», Москва, 1968.

4. Крейн С.Г., Петунин Ю.И., Семенов Е.М. Интерполяция линейных операторов.«Наука», Москва, 1978.

5. Натансон И.П. Теория функций вещественной переменной. «Наука», Москва, 1974.

Распространим меру с сохранением свойств 1 и 2, определенную пока для сегментов, на более широкий класс множеств – так называемые элементарные множества.

Назовем множество элементарным, если его можно представить хотя бы одним способом как объединение конечного числа попарно непересекающихся сегментов.

Определим теперь меру для элементарных множеств следующим образом: если , где - попарно непересекающиеся сегменты, то .

 Скачать реферат